Home
Class 9
MATHS
ABC is a triangle. Locate a point in the...

ABC is a triangle. Locate a point in the interior of `triangle` ABC which is equidistant from all the vertices of `triangle` ABC

Text Solution

Verified by Experts

The correct Answer is:
PC
Promotional Banner

Topper's Solved these Questions

  • TRIANGLES

    KUMAR PRAKASHAN|Exercise SKILL TESTING EXERCISE|20 Videos

  • TRIANGLES

    KUMAR PRAKASHAN|Exercise MULTIPLE CHOICE QUESTIONS|15 Videos

  • TRIANGLES

    KUMAR PRAKASHAN|Exercise EXERCISE 7.4|6 Videos

  • SURFACE AREAS AND VOLUMES

    KUMAR PRAKASHAN|Exercise MULTIPLE CHOICE QUESTIONS|18 Videos

Similar Questions

Explore conceptually related problems

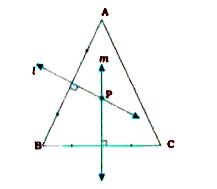
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.

In triangle ABC and triangle DEF, AB = DE, BC = EF and angleB = angleE . If the perimeter of triangle ABC is 20, then the perimeter of triangle DEF is ..........

ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is

Construct a triangle similar to the given Delta ABC , with its sides equal to (5)/(3) of the corresponding sides of the triangle ABC.

ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that ( i ) triangle ABE ~= triangle ACF (ii) AB = AC i.e ABC is an isoceles triangle

D is a point on side BC of triangle ABC such that AD = AC (see the given figure). Show that AB gt AD.

In triangle ABC, AD is a median. Prove that AB + AC gt 2AD

Draw a triangle ABC with side BC= 6 cm. AB=5 cm and angle ABC = 60^(@). Then sonstruct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC

let ABC be a right angled triangle at C. If the inscribed circle touches the side AB at D and (AD) (BD)=11, then find the area of triangle ABC. .

In triangle ABC, AB = AC and the bisector of angle A lt intersects BC at D. Prove that, ( 1 ) triangle ADB = triangle ADC ( 2 ) angle ABC = angle ACB