To solve the problem of determining the velocity of a pebble dropped into viscous oil as a function of time, we can analyze the forces acting on the pebble and how they affect its motion. Here’s a step-by-step breakdown:
### Step 1: Understand the Forces Acting on the Pebble
When the pebble is dropped into the viscous oil, two main forces act on it:
- The gravitational force (downward): \( F_g = mg \)
- The viscous drag force (upward): \( F_d = 6 \pi \eta r v \)
Where:
- \( m \) is the mass of the pebble,
- \( g \) is the acceleration due to gravity,
- \( \eta \) is the viscosity of the oil,
- \( r \) is the radius of the pebble,
- \( v \) is the velocity of the pebble.
### Step 2: Analyze the Motion of the Pebble
Initially, when the pebble is dropped, its velocity \( v = 0 \). At this moment, the viscous drag force is also zero, and the only force acting on the pebble is the gravitational force. This means the pebble will start accelerating downwards.
### Step 3: Determine the Acceleration
As the pebble accelerates, the viscous drag force begins to increase with the velocity. The net force acting on the pebble can be expressed as:
\[ F_{net} = mg - F_d \]
Using Newton's second law, we can write:
\[ ma = mg - 6 \pi \eta r v \]
Where \( a \) is the acceleration of the pebble.
### Step 4: Terminal Velocity
As time progresses, the velocity of the pebble increases, which in turn increases the viscous drag force. Eventually, the viscous drag force will equal the gravitational force, and the net force will become zero. This condition is known as terminal velocity \( v_t \), where:
\[ mg = 6 \pi \eta r v_t \]
At this point, the pebble will stop accelerating and continue to fall at a constant velocity (terminal velocity).
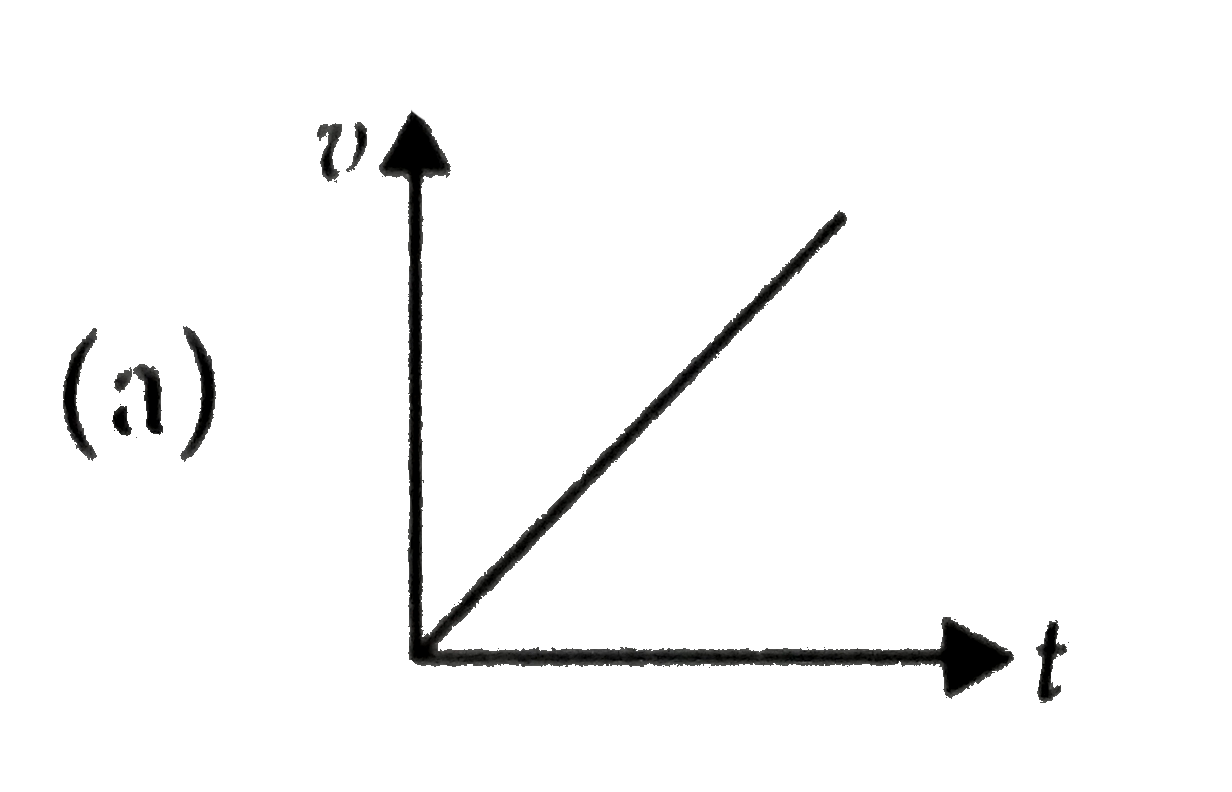
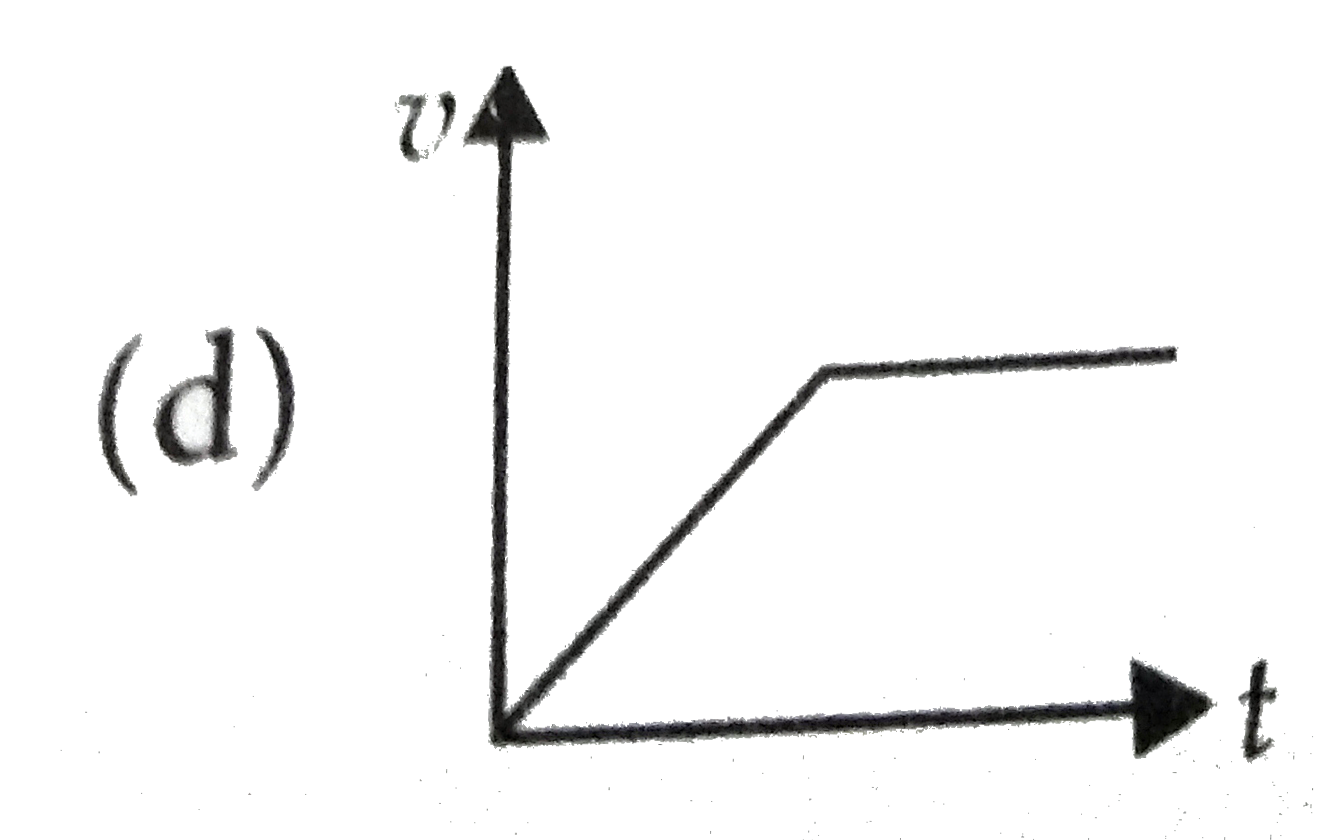
### Step 5: Sketch the Velocity vs. Time Graph
From the analysis:
- Initially, the velocity increases rapidly as the pebble accelerates.
- As the pebble approaches terminal velocity, the rate of increase of velocity decreases.
- Finally, the velocity levels off as the pebble reaches terminal velocity.
Therefore, the graph of velocity \( v \) as a function of time \( t \) will start at zero, rise quickly, and then gradually level off as it approaches terminal velocity.
### Conclusion
Based on this analysis, the correct graph that represents the velocity of the pebble as a function of time is the one that shows an initial steep increase followed by a gradual leveling off, indicating the approach to terminal velocity.