Home
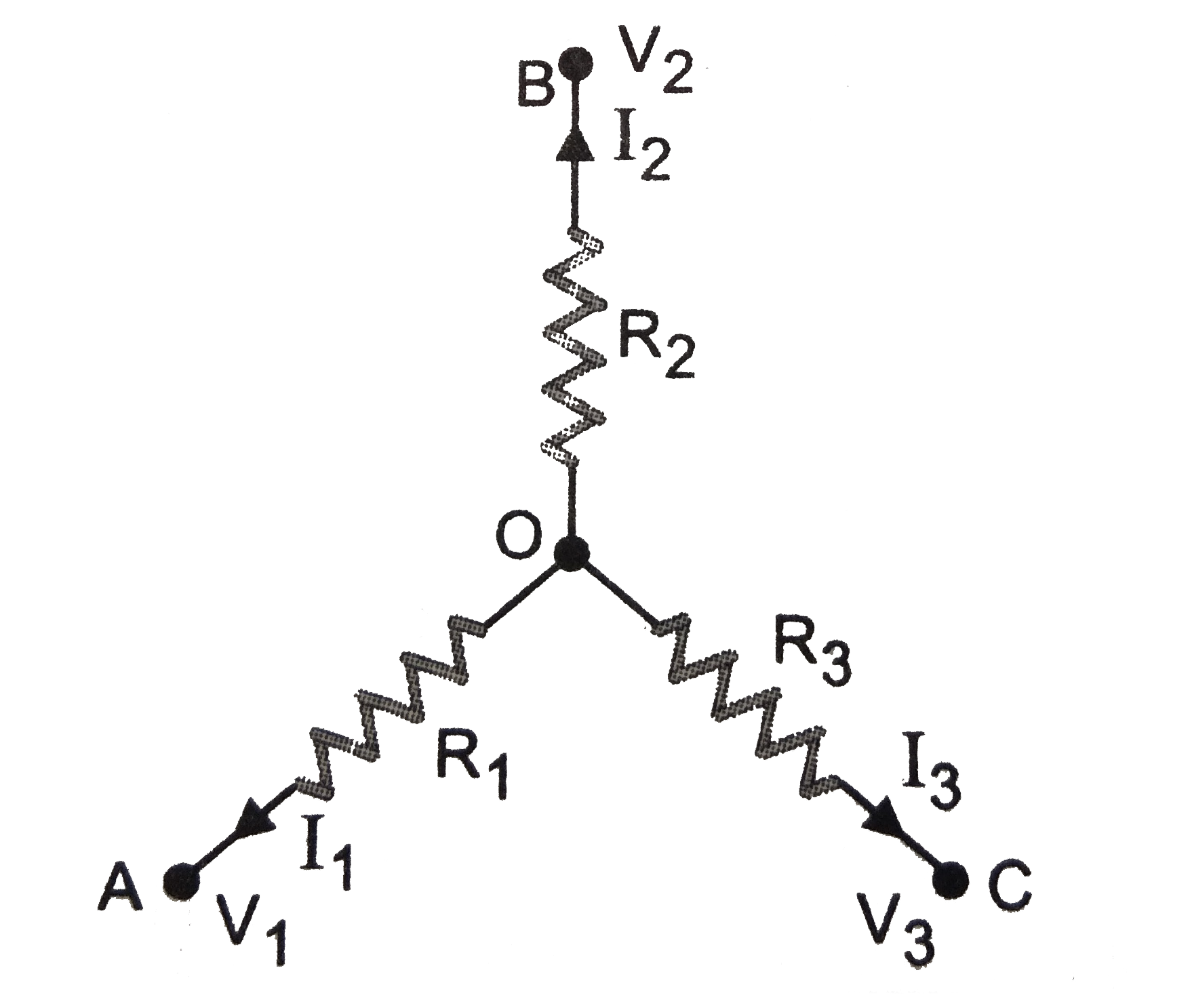
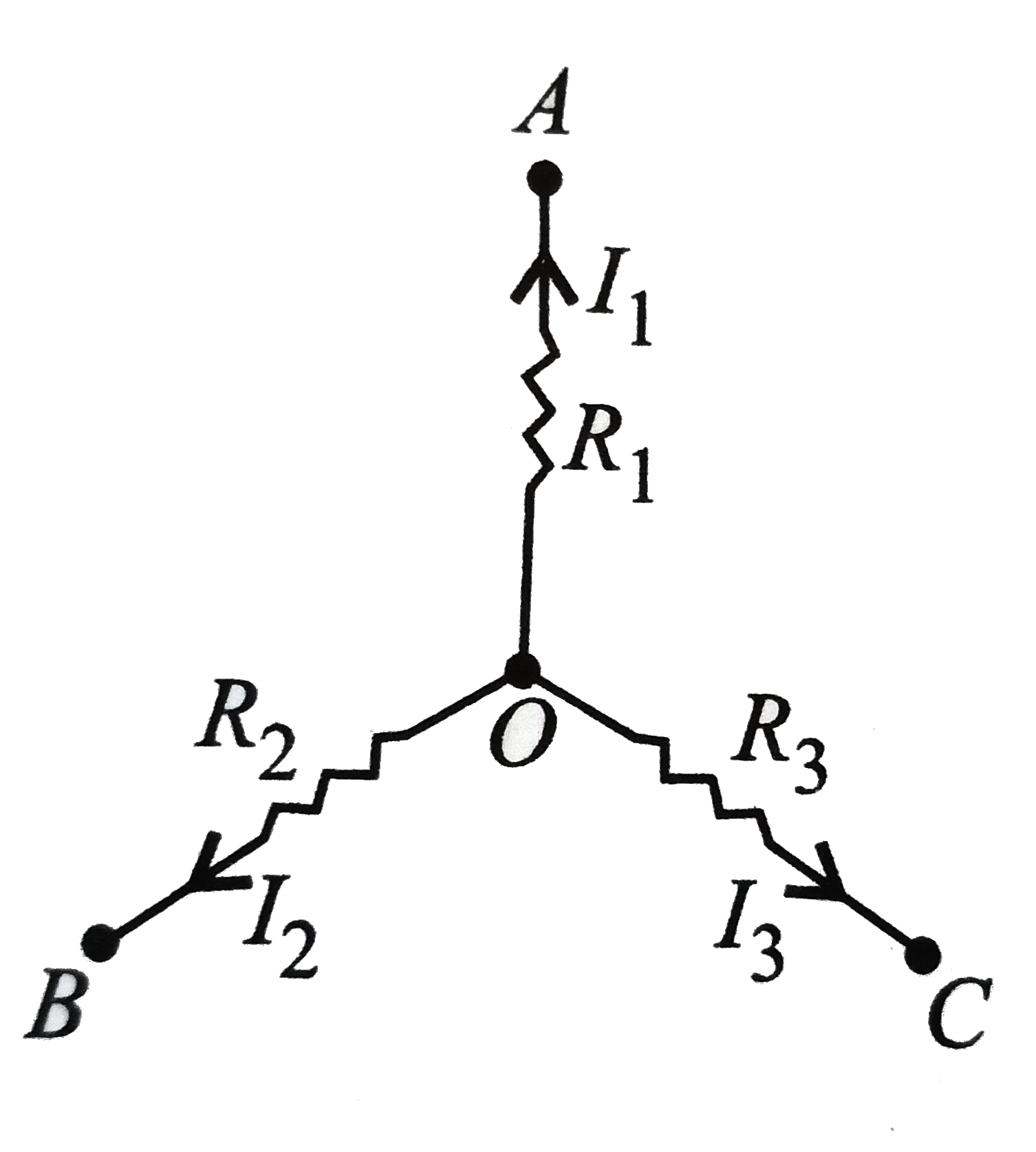
Class 12
PHYSICS
A circuit has a section ABC if the poten...

A circuit has a section `ABC` if the potential at point `A,B and C` are `V_(1) , V_(2) and V_(3)` respectively , calculate the potential at point `O`

A

`V_(1)+V_(2)+V_(3)`

B

`[(V_(1)+V_(2)+V_(3))/(R_(1)+R_(2)+R_(3))][(1)/(R_(1)+R_(2)+R_(3))]^(-1)`

C

zero

D

`[(V_(1)+V_(2)+V_(3))/(R_(1)+R_(2)+R_(3))](R_(1)+R_(2)+R_(3))`

Text Solution

Verified by Experts

The correct Answer is:
B
Applying juction rule `-I_(1)-I_(2)-I_(3)=0`
i.e., `I_(1)+I_(2)+I_(3)=0…(i)`
Let, `V_(0)` bet the potential at point O. By Ohm's law for resistance, `R_(1),R_(2) and R_(3)` respectively, we get
`(V_(0)-V_(1))=I_(1)R_(1),(V_(0)-V_(2))=I_(2)R_(2) and (V_(0)-V_(3))=I_(3)R_(3)`
`or I_(1)=((V_(0)-V_(1)))/(R_(1)), I_(2)=((V_(0)-V_(2)))/(R_(2)), I_(3)=((V_(3)-V_(3)))/(R_(3))`
So substituting these values of `I_(1),I(2) and I_(3)` in eq. (i) , we get
`V_(0)[(1)/(R_(1))+(1)/R_(2)+(1)/(R_(3))]-[(V_(1))/(R_(1))+(V_(2))/(R_(2))+(V_(3))/(R_(3))]=0`
`V_(0)=[(V_(1))/(R_(1))+(V_(2))/(R_(2))+(V_(3))/(R_(3))] [(1)/(R_(1))+(1)/R_(2)+(1)/(R_(3))]^(1)`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • CURRENT ELECTRICITY

    NCERT FINGERTIPS ENGLISH|Exercise WHEATSTONE BRIDGE|6 Videos

  • CURRENT ELECTRICITY

    NCERT FINGERTIPS ENGLISH|Exercise METER BRIDGE|4 Videos

  • CURRENT ELECTRICITY

    NCERT FINGERTIPS ENGLISH|Exercise CELLS, EMF, INTERNAL RESISTANCE|6 Videos

  • COMMUNITCATION SYSTEMS

    NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|30 Videos

  • DUAL NATURE OF RADIATION AND MATTER

    NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|15 Videos

Similar Questions

Explore conceptually related problems

The arrangement shows a part of complete circuit. The potentials at point A and B are V_(1) and V_(2) respectively . Find the potential at point P. Strategy : The two capacitors C_(1) and C_(2) are connected in series . Therefore the charge on both of the capacitors is same . Let the potential at P is V .

Three resistance are joined together to form a letter Y, as shown in figure. If the potentials of the terminals A, B and C are 6V, 3V and 2V respectively, then the potential of the point O will be

Three capacitors C_(1),C_(2) and C_(3) are connected as shown in, The potentials of P,Q , and R are V_(1),V_(2), and V_(3) , respectively. Find the potential V_(0) at the function O . .

The arrangement shows a part of complete circuit . The potentials at points A and B are V_(1) and V_(2) respectively . Find the potential at point P . Strategy : The two capacitors C_(1) and C_(2) are connected in series . Therefore the charge on both of the capacitors is same. Let the potential at P is V.

Three uncharged capacitors are connected as shown in the figure. If potentials at point P, Q and R are maintained at 1V, 2V, 3V respectively, then potential at O becomes .

The electric field and the electric potential at a point are E and V respectively.

A network of resistance is constructed with R_1 and R_2 as shown in fig. The potential at the points 1,2,3 …., N are V_1, V_2,V_3,…,V_n, respectively, each having a potential k times smaller then the previous one. The ratio R_1//R_2 is

shows two capacitors in series, the rigid central conducting section of length b being movable vertically. . If the potentials of the upper and lower plates are V_(1) and V_(2) respectively, then potebtial of rigid segid secton is.

Mass M is uniformly distributed only on curved surface of a thin hemispherical shell. A, B and C are three points on the circular base of hemisphere, such that A is the centre. Let the gravitational potential at poins A, B and C be V_(A), V_(B), V_(C) respectively. Then :

In the circuit shown, what is the potential different V_(PQ) ?

Home
Profile