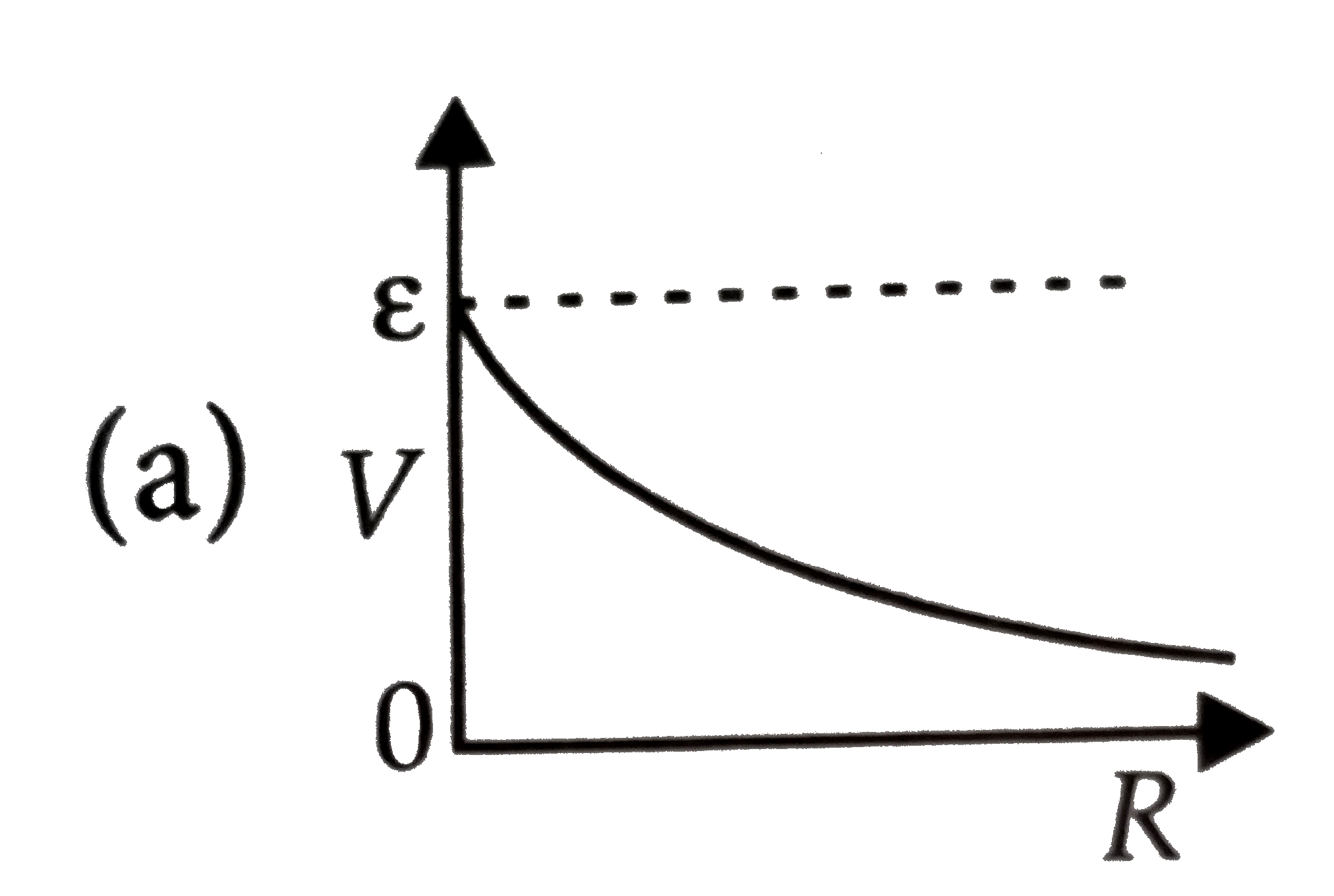
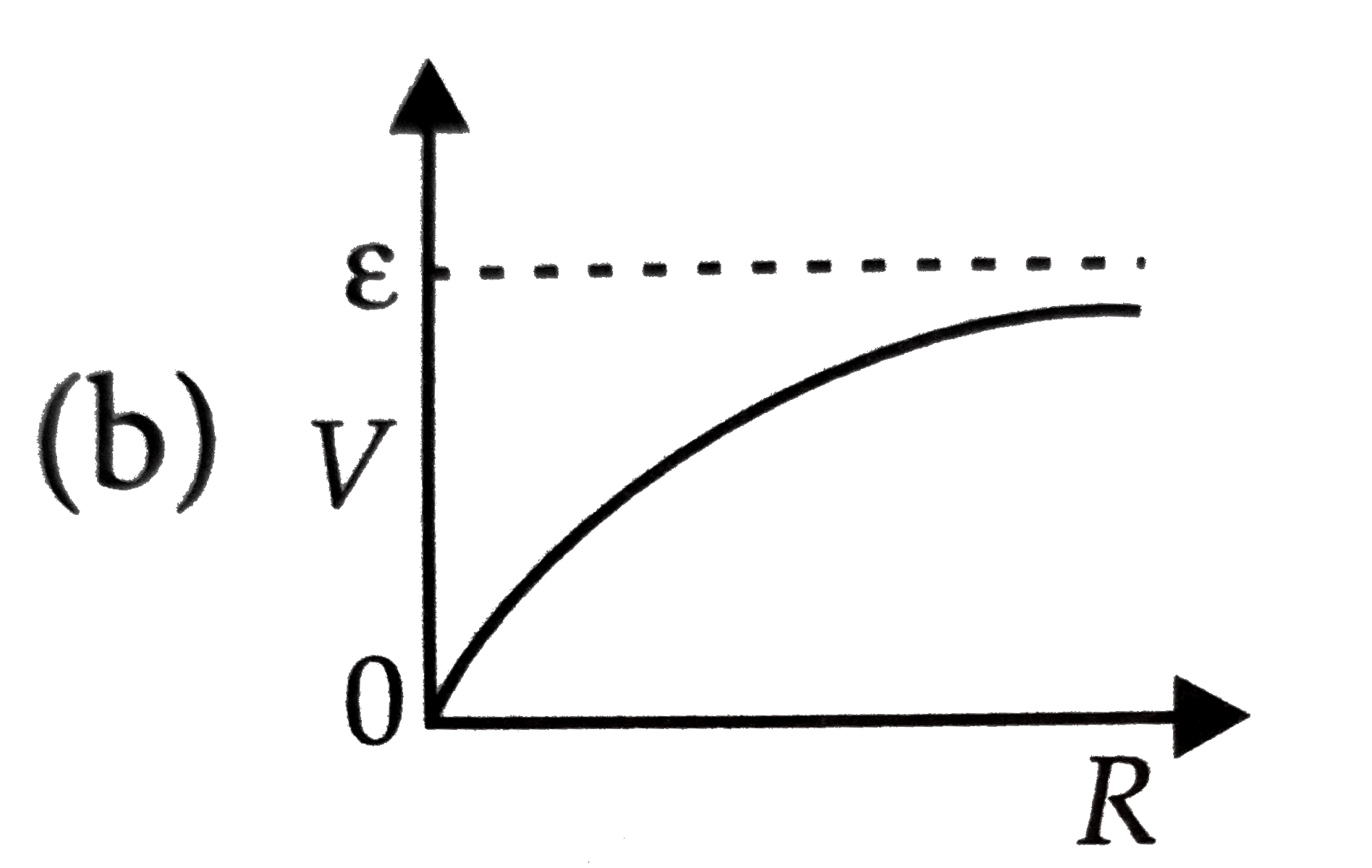
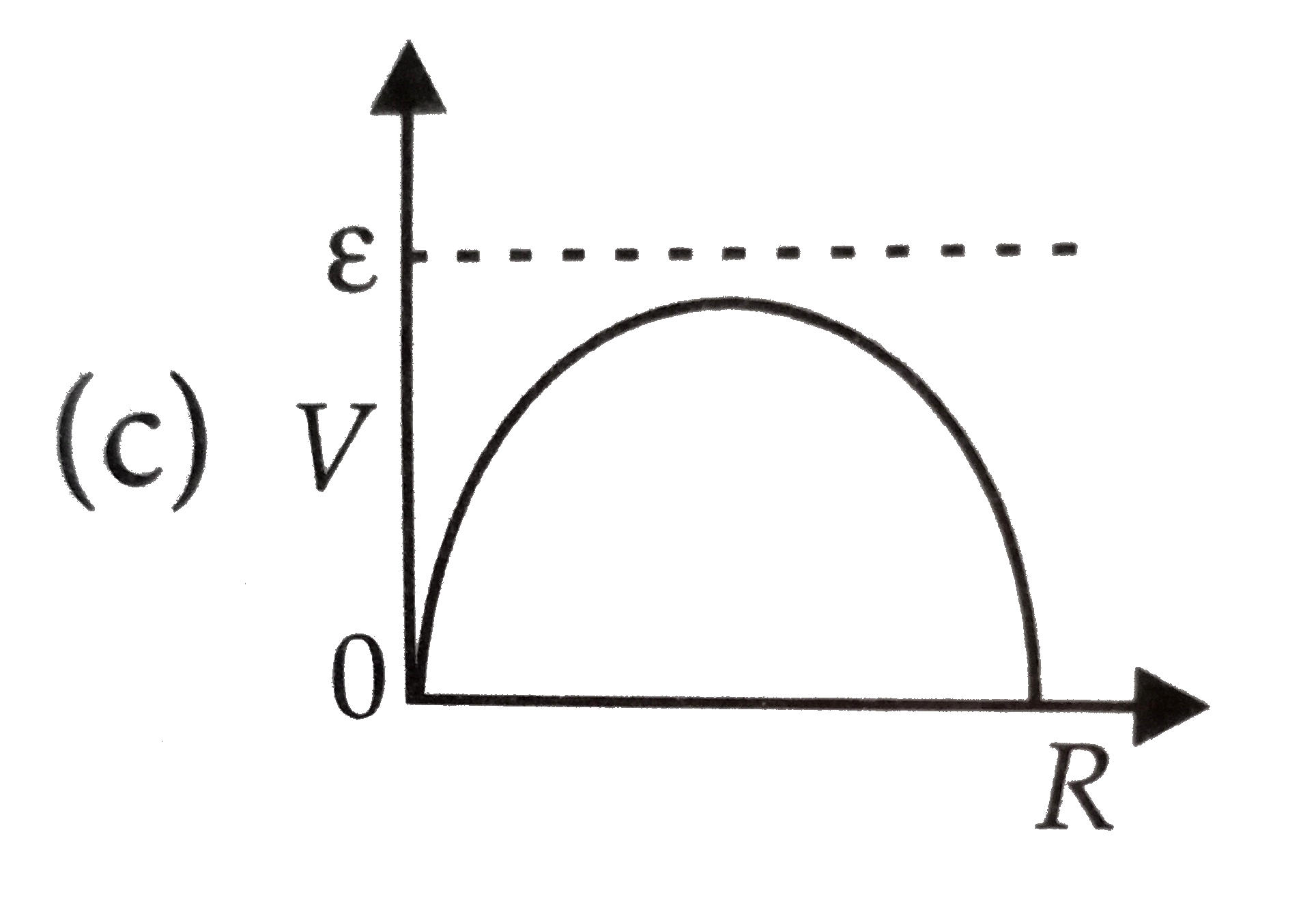
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
CURRENT ELECTRICITY
NCERT FINGERTIPS ENGLISH|Exercise KIRCHOFF S LAW|14 VideosCURRENT ELECTRICITY
NCERT FINGERTIPS ENGLISH|Exercise WHEATSTONE BRIDGE|6 VideosCURRENT ELECTRICITY
NCERT FINGERTIPS ENGLISH|Exercise COMBINED OF RESISTORS;|23 VideosCOMMUNITCATION SYSTEMS
NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|30 VideosDUAL NATURE OF RADIATION AND MATTER
NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|15 Videos
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS ENGLISH-CURRENT ELECTRICITY-CELLS, EMF, INTERNAL RESISTANCE
- A cell having an emf E and internal resistance r is connected across a...
Text Solution
|
- A battery of emf 15 V and internal resistance of 4Omega is connected ...
Text Solution
|
- The battery of a trunk has an emf of 24 V. If the internal resistance ...
Text Solution
|
- A battery having 12V emf and internal resistance 3Omega is connected t...
Text Solution
|
- When a current of 2 A flows in a battery from negative to positive ter...
Text Solution
|
- In a circuit a cell with internal resistance r is connected to an exte...
Text Solution
|