Home
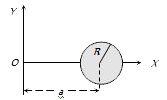
Class 11
PHYSICS
The adjoining figure shows a disc of mas...

The adjoining figure shows a disc of mass M and radius R lying in the X-Y plane with its centre on X - axis at a distance a from the origin. Then the moment of inertia of the disc about the X-axis is

A

`M((R^(2))/(2))`

B

`M((R^(2))/(4))`

C

`M((R^(2))/(4)+a^(2))`

D

`M((R^(2))/(2)+a^(2))`

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • ROTATIONAL MOTION

    ERRORLESS |Exercise Practice Problems (Problems based on angular momentum)|16 Videos

  • ROTATIONAL MOTION

    ERRORLESS |Exercise Practice Problems (Problems based on kinetic energy, work and power)|30 Videos

  • ROTATIONAL MOTION

    ERRORLESS |Exercise Practice Problems (Problems based on torque, couple)|11 Videos

  • NEWTONS LAWS OF MOTION

    ERRORLESS |Exercise Self Evaluation Test|16 Videos

  • SIMPLE HARMONIC MOTION

    ERRORLESS |Exercise simple Harmonic Motion|21 Videos

Similar Questions

Explore conceptually related problems

A uniform disc (of mass M and radius a ) has a hole (of radius b ) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?

A uniform circular disc of radius R lies in the XY plane with its centre coinciding with the origin.The moment of inertia about an axis passing through a point on the X-axis at a distance x=2R and perpendicular to the X-Y plane is equal to its moment of inertia about an axis passing through a pint on the Y-axis at a distance y=d and parallel to the X-axis in the X-Y plane. The value of d is

If the radius of gyration of a solid disc of mass 10 kg about an axis is 0.40 m, then the moment of inertia of the disc about that axis is

The moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is

A solid sphere of mass M and radius R having moment of inertial I about its diameter is recast into a solid disc of radius r and thickness t .The moment of inertia of the disc about an axis passing the edge and perpendicular to the plane remains "I" .Then r=(x)/(sqrt(15))R Find x=?

Moment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R . The value of x is

A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -

A small hole is made in a disc of mass M and radius R at a distance R//4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is

A uniform disc of radius R lies in the x-y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y = x + c . The value of c will be. .

The moment of inertia of a uniform circular disc of mass M and radius R about any of its diameters is 1/4 MR^(2) . What is the moment of inertia of the disc about an axis passing through its centre and normal to the disc?

ERRORLESS -ROTATIONAL MOTION-Practice Problems (Problems based on moment of inertia)
  1. Three identical thin rods each of length l and mass M are joined toget...

    Text Solution

    |

  2. Moment of inertia of a sphere of mass M and radius R is I. Keeping M ...

    Text Solution

    |

  3. Three particles are situated on a light and rigid rod placed along Y-a...

    Text Solution

    |

  4. On account of melting of ice at the north pole the moment of inertia o...

    Text Solution

    |

  5. According to the theorem of parallel axes I = I("cm") + Mx^(2), the g...

    Text Solution

    |

  6. What is the moment of inertia of a square sheet of side l and mass pe...

    Text Solution

    |

  7. The adjoining figure shows a disc of mass M and radius R lying in the ...

    Text Solution

    |

  8. We have two spheres, one of which is hollow and the other solid. They ...

    Text Solution

    |

  9. From a uniform wire, two circular loops are made (i) P of radius r and...

    Text Solution

    |

  10. One quarter sector is cut from a uniform circular disc of radius R. Th...

    Text Solution

    |

  11. Two discs of same thickness but of different radii are made of two dif...

    Text Solution

    |

  12. A thin wire of length L and uniform linear mass density rho is bent in...

    Text Solution

    |

  13. If a solid sphere and solid cylinder of same mass and radius rotate ab...

    Text Solution

    |

  14. Two point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of...

    Text Solution

    |

  15. A circular disc A of radius r is made from an iron plate of thickness ...

    Text Solution

    |

  16. A thin wire of length l and mass m is bent in the form of a semicircle...

    Text Solution

    |

  17. If l(1) is the moment of inertia of a thin rod about an axis perpendic...

    Text Solution

    |

  18. Four solids are shown in cross section. The sections have equal height...

    Text Solution

    |

  19. The moment of inertia l of a solid sphere having fixed volume depends ...

    Text Solution

    |

  20. A thin rod of length L of mass M is bent at the middle point O at an a...

    Text Solution

    |