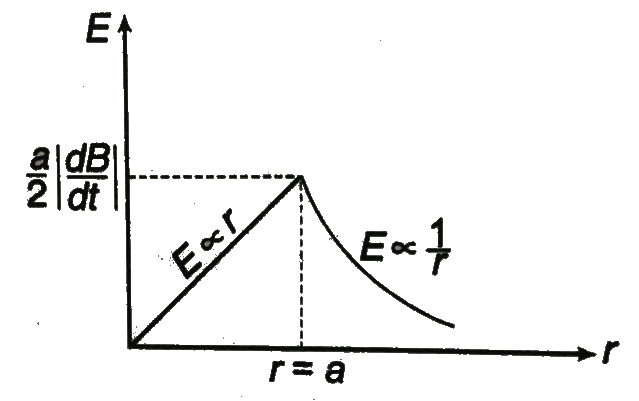
A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
DC PANDEY ENGLISH|Exercise Example Type 6|3 VideosELECTROMAGNETIC INDUCTION
DC PANDEY ENGLISH|Exercise Miscellaneous Examples|5 VideosELECTROMAGNETIC INDUCTION
DC PANDEY ENGLISH|Exercise Example Type 4|2 VideosCURRENT ELECTRICITY
DC PANDEY ENGLISH|Exercise Medical entrances gallery|97 VideosELECTROMAGNETIC WAVES
DC PANDEY ENGLISH|Exercise Sec C|22 Videos
Similar Questions
Explore conceptually related problems