A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCULAR MOTION
DC PANDEY ENGLISH|Exercise More than One Option is Correct|13 VideosCIRCULAR MOTION
DC PANDEY ENGLISH|Exercise Comprehension|13 VideosCIRCULAR MOTION
DC PANDEY ENGLISH|Exercise JEE Main|23 VideosCENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
DC PANDEY ENGLISH|Exercise Level 2 Subjective|21 VideosCOMMUNICATION SYSTEM
DC PANDEY ENGLISH|Exercise Only One Option is Correct|27 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-CIRCULAR MOTION-JEE Advanced
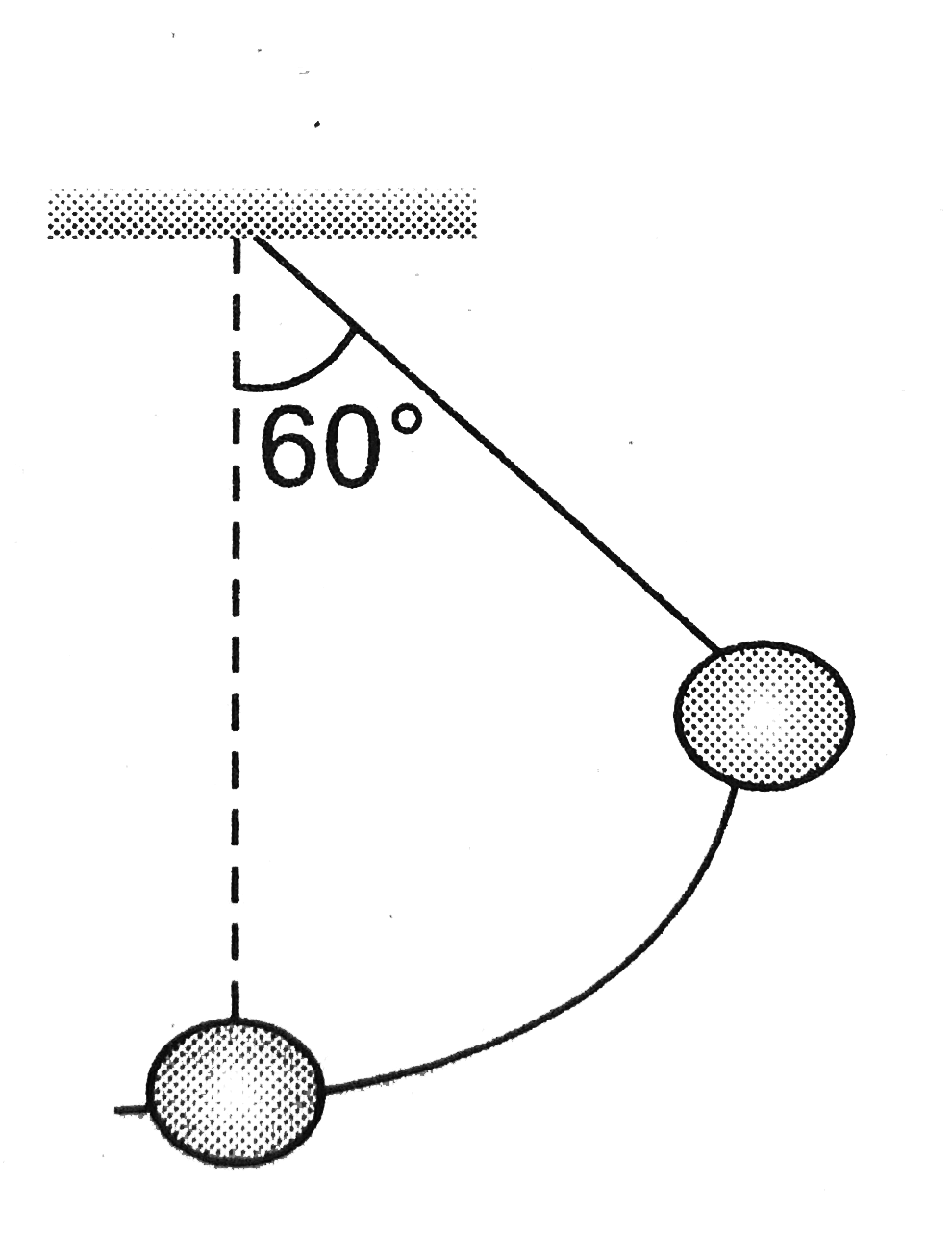
- A pendulum of length l=1m is released from theta(0)=60^(@) . The rate ...
Text Solution
|
- A particle starts traveling on a circle with constant tangential accel...
Text Solution
|
- A block of mass m is placed inside a smooth hollow cylinder of radius ...
Text Solution
|
- A simple pendulum is vibrating with an angular amplitude of 90^(@) as ...
Text Solution
|
- A ball of mass m is attached to one end of a light rod of length l, th...
Text Solution
|
- A particle is given an intial speed u inside a smooth spherical shell ...
Text Solution
|
- A bob is suspended from a crane by a cable of length l=5m . The crane ...
Text Solution
|
- A smooth sphere of radius R is made to translate line with a constant ...
Text Solution
|
- Two bodies of masses m and 4 m are attached with string as shown in th...
Text Solution
|
- Two beads A and B of equal mass m are connected by a light inextensibe...
Text Solution
|
- A small block of mass m is released from rest from point A inside a sm...
Text Solution
|
- An automobile enters a turn whose radius is R. The road is banked at a...
Text Solution
|
- A ball of mass 1 kg is released from position A inside a wedge with a ...
Text Solution
|
- A partical of mass m oscillates along the horizontal diameter AB insi...
Text Solution
|
- A bead of mass m is attached to one end of a spring of natural length ...
Text Solution
|
- A particle is moving in a circular path. The acceleration and momentum...
Text Solution
|
- A ball of mass 'm' is rotating in a circle of radius 'r' with speed v...
Text Solution
|
- A block of mass m=1kg has a speed v = 4 m//s at theta = 60^(@) on a ci...
Text Solution
|
- Two blocks of masses 1 kg and 2 kg are joined by a massless inextensib...
Text Solution
|
- Two different blocks of equal mass m are released from two positions a...
Text Solution
|