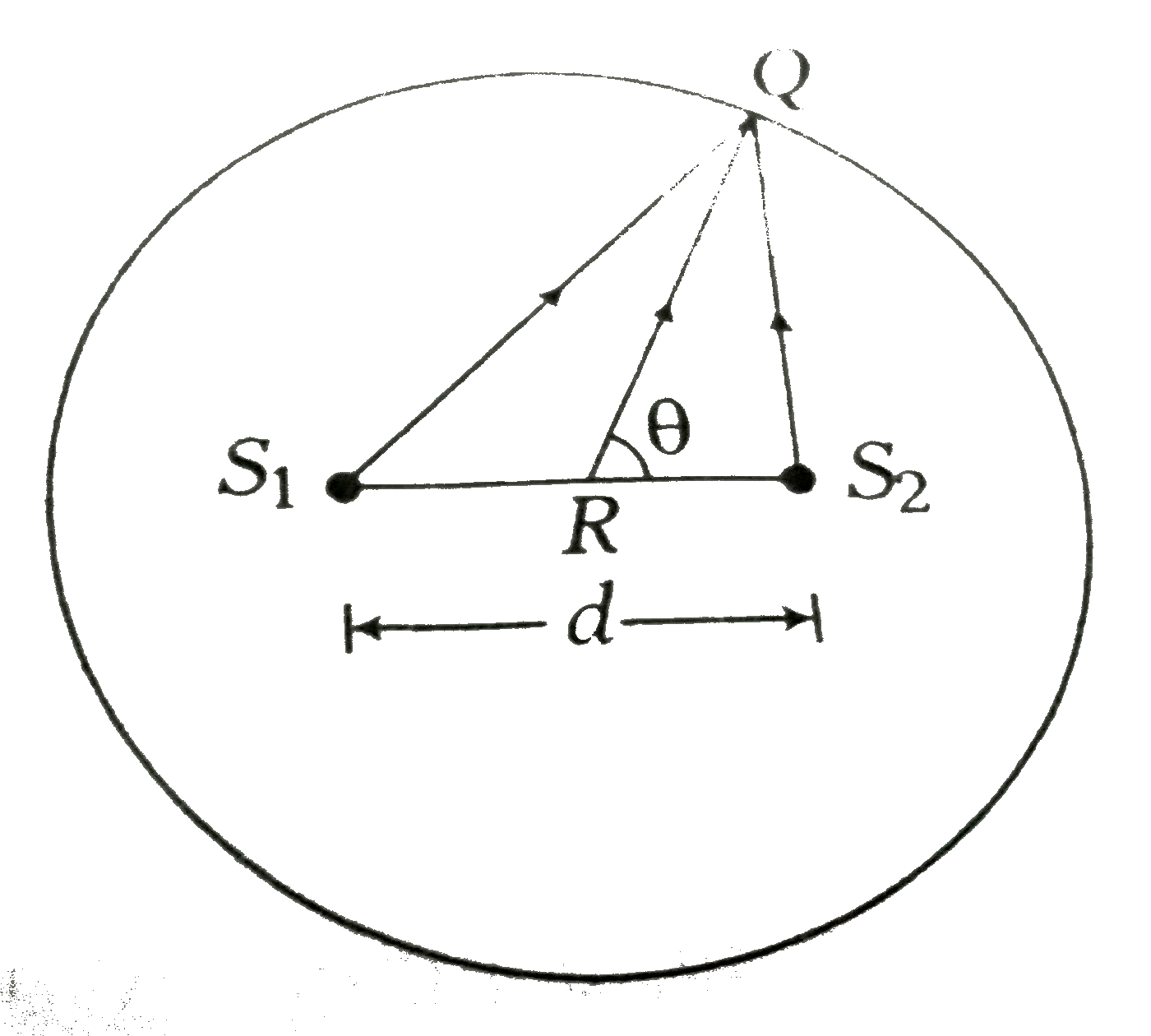
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
WAVE OPTICS
DC PANDEY ENGLISH|Exercise Assertion reason|8 VideosView PlaylistWAVE OPTICS
DC PANDEY ENGLISH|Exercise match column|4 VideosView PlaylistWAVE OPTICS
DC PANDEY ENGLISH|Exercise Check point|65 VideosView PlaylistSOLVED PAPERS 2018
DC PANDEY ENGLISH|Exercise JIPMER|22 VideosView Playlist
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-WAVE OPTICS-taking it together
- In Young's double slit experiment the y-coordinates of central maxima ...
03:31
|
Play - In Young's double slit experiment, wavelength lambda=5000Å the distanc...
03:20
|
Play - A parallel beam of light of intensity I is incident on a glass plate. ...
02:58
|
Play - In the Young's double slit experiment, the intensities at two points P...
04:30
|
Play - A monochromatic beam of light fall on YDSE apparatus at some angle (sa...
04:56
|
Play - Figure shows a standard two slit arrangement with slits S(1), S(2). P(...
02:25
|
Play - In Young's double slit experiment, the two slits acts as coherent sour...
06:30
|
Play - In the ideal double-slit experiment, when a glass-plate (refractive in...
01:49
|
Play - In the standard Young's double slit experiment, the intensity on the s...
04:16
|
Play - In a Young's double slit experiment, D equals the distance of screen a...
04:25
|
Play - White light is used to illuminate the two slits in a Young's double sl...
03:37
|
Play - The intensity of each of the two slits in Young's double slit experime...
06:19
|
Play - In a double-slit experiment, fringes are produced using light of wavel...
03:52
|
Play - An interference is observed due to two coherent sources S1 placed at o...
03:22
|
Play - Intensity at centre in YDSE is l(0) if one slit is covered. Then inten...
01:29
|
Play - Two coherent light sources A and B are at a distance 3lambda from each...
02:37
|
Play - Two coherent sources separated by distance d are radiating in phase ha...
02:59
|
Playing Now - Consider a ray of light incident from air onto a slab of glass (refrac...
07:13
|
Play - Two ideal slits S(1) and S(2) are at a distance d apart, and illuninat...
04:17
|
Play - For the given incident ray as shown in figure, the condition of total ...
02:45
|
Play