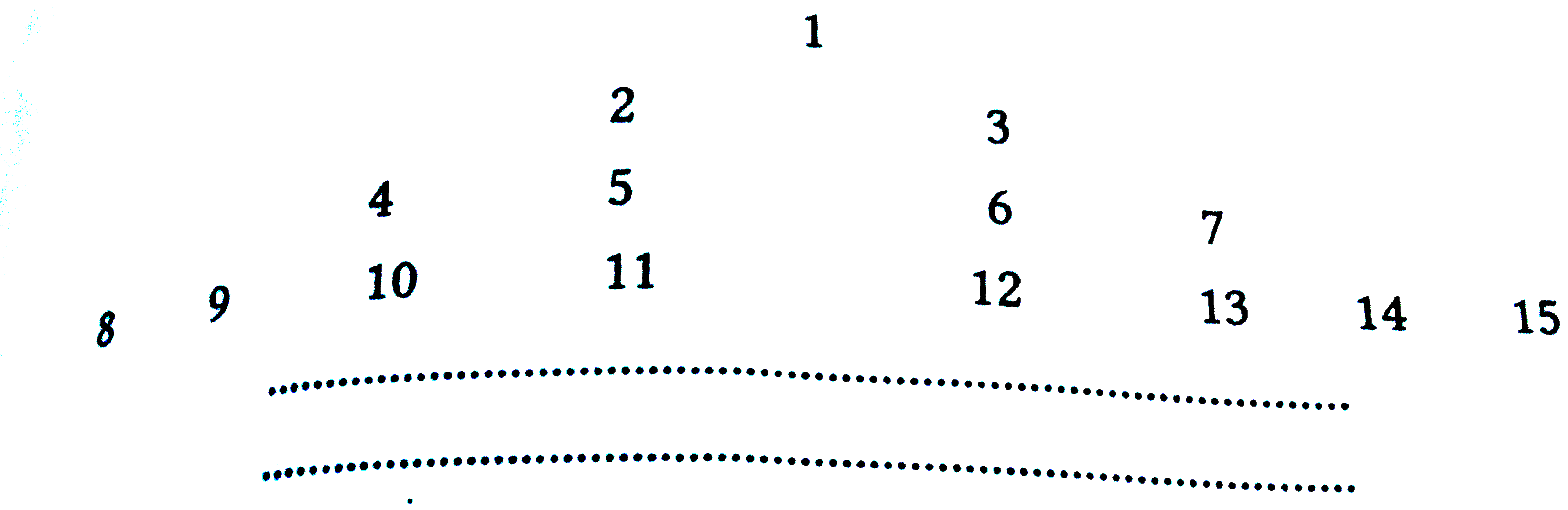Text Solution
Verified by Experts
|
Topper's Solved these Questions
SEQUENCES AND SERIES
ARIHANT MATHS ENGLISH|Exercise Exercise For Session 1|5 VideosView PlaylistSEQUENCES AND SERIES
ARIHANT MATHS ENGLISH|Exercise Exercise For Session 2|11 VideosView PlaylistPROPERTIES AND SOLUTION OF TRIANGLES
ARIHANT MATHS ENGLISH|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|21 VideosView PlaylistSETS, RELATIONS AND FUNCTIONS
ARIHANT MATHS ENGLISH|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|12 VideosView Playlist
Similar Questions
Explore conceptually related problems
ARIHANT MATHS ENGLISH-SEQUENCES AND SERIES-Exercise (Questions Asked In Previous 13 Years Exam)
- The natural numbers arearranged innthe form given below The rth ...
04:03
|
Playing Now - Let a,b,c be in A.P. and |a|lt1,|b|lt1|c|lt1.ifx=1+a+a^(2)+ . . . ."to...
02:07
|
Play - about to only mathematics
06:12
|
Play - If a1, a2, a3, be terms of an A.P. and (a1+a2+.....+ap)/(a1+a2+.....+...
05:38
|
Play - If a1, a2, a3,.....an are in H.P. and a1 a2+a2 a3+a3 a4+.......a(n-1...
05:30
|
Play - Let V(r ) denotes the sum of the first r terms of an arithmetic progre...
06:43
|
Play - Let Vr denote the sum of the first r terms of an arithmetic progressio...
06:43
|
Play - Let V(r) denote the sum of the first r terms of an arithmetic progress...
05:37
|
Play - LetA(1),G(1),H(1) denote the arithmetic, geometric and harmonic means ...
05:08
|
Play - Let A1 , G1, H1denote the arithmetic, geometric and harmonic means re...
05:08
|
Play - LetA(1),G(1),H(1) denote the arithmetic, geometric and harmonic means ...
05:08
|
Play - In a G.P of positive terms if any term is equal to the sum of the next...
03:35
|
Play - Suppose four distinct positive numbers a(1),a(2),a(3),a(4) are in G.P....
02:54
|
Play - The first two terms of a geometric progression add up to 12. The sum o...
02:58
|
Play - If the sum of first n terms of an A.P. is cn^(2) then the sum of squar...
05:31
|
Play - The sum to infinity of the series 1+2/3+6/3^2+14/3^4+...is
04:53
|
Play - Let Sk,k=1, 2, …. 100 denote the sum of the infinite geometric series ...
02:32
|
Play - Let a1, a2, a3, ,a(11) be real numbers satisfying a1=15 , 27-2a2>0 a ...
13:20
|
Play - A person is to count 4500 currency notes. Let an denote the number of ...
02:55
|
Play - The minimum value of the sum of real numbers a^-5, a^-4, 3a^-3, 1,a^8 ...
02:02
|
Play - A man saves ₹ 200 in each of the first three months of his servies.In ...
02:41
|
Play