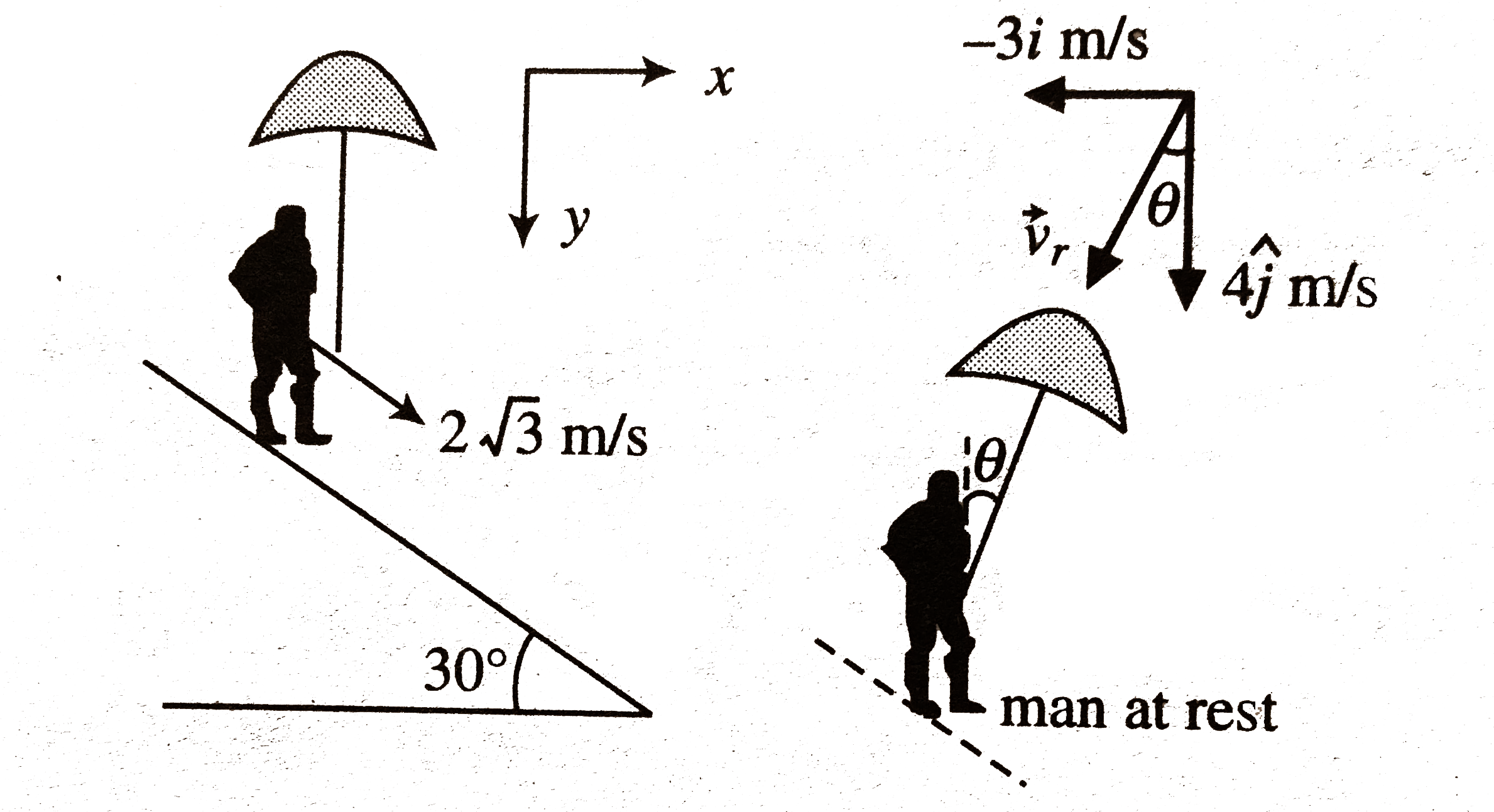Text Solution
Verified by Experts
|
Topper's Solved these Questions
KINEMATICS-2
CENGAGE PHYSICS ENGLISH|Exercise Solved Examples|7 VideosView PlaylistKINEMATICS-2
CENGAGE PHYSICS ENGLISH|Exercise Exercise 5.1|15 VideosView PlaylistKINEMATICS-1
CENGAGE PHYSICS ENGLISH|Exercise Integer|9 VideosView PlaylistKINETIC THEORY OF GASES
CENGAGE PHYSICS ENGLISH|Exercise Compression|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-KINEMATICS-2-Exercise Integer
- A man is coming down an incline of angle 30^@. When he walks with spee...
07:09
|
Playing Now - A particle is projected with velocity u at angle theta with horizontal...
03:24
|
Play - From a tower of height 40 m, two bodies are simultaneously projected h...
03:39
|
Play - A bead is free to slide down on a smooth wire rightly stretched betwee...
03:14
|
Play - A golfer standing on the ground hits a ball with a velocity of 52 m//s...
06:20
|
Play - A body is thrown with the velocity v0 at an angle of theta to the hori...
02:16
|
Play - A boy standing on a long railroad car throws a ball straight upwards. ...
03:18
|
Play - A staircase contains three steps each 10 cm high and 20 cm wide figure...
04:46
|
Play - A particle is projected up an inclined plane of inclination beta at an...
02:52
|
Play - A particle is moving in a circle of radius R with constant speed. The ...
06:24
|
Play
 .
.