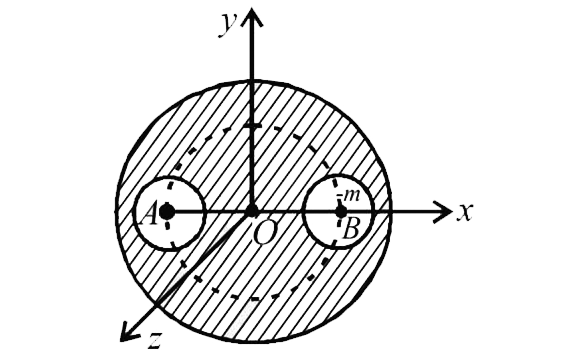
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise AR_TYPE|1 VideosGRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 VideosGRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise SCQ_TYPE|12 VideosFLUID MECHANICS
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 VideosKINEMATICS-1
CENGAGE PHYSICS ENGLISH|Exercise Integer|9 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-GRAVITATION-MCQ_TYPE
- A solid sphere of uniform density and radius 4 units is located with i...
Text Solution
|
- The magnitudes of the gravitational force at distances r(1) and r(2) f...
Text Solution
|
- A satellite S is moving in an elliptical orbit around the earth. The m...
Text Solution
|
- Two spherical planets P and Q have the same uniform density rho, masse...
Text Solution
|