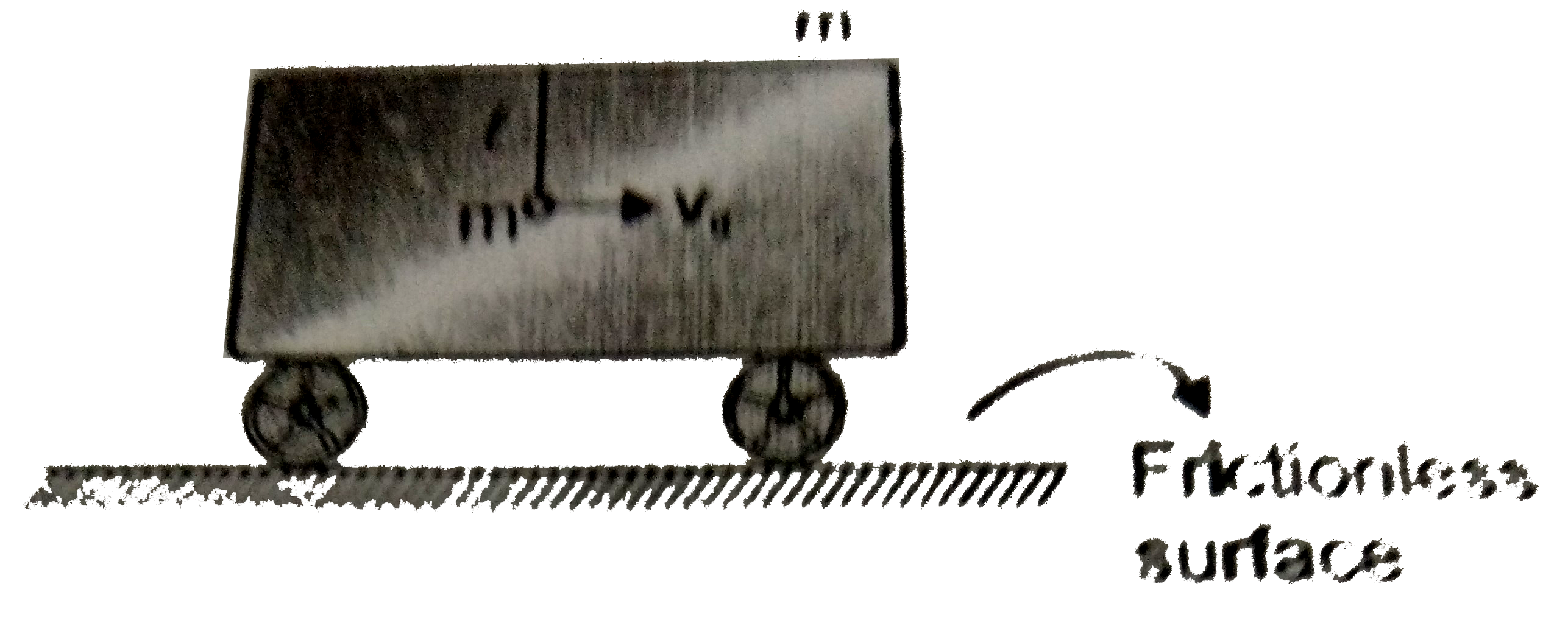
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 54|8 VideosView PlaylistDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise DPP 55|8 VideosView PlaylistDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 52|7 VideosView PlaylistCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise Exercise|53 VideosView PlaylistELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Advanced Level Problems|9 VideosView Playlist
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEMS-dpp 53
- A small bob mass 'm' is suspended by a massless string from a cart of ...
04:45
|
Playing Now - In the figure shown, coefficient of restitution between A and B is e=1...
06:40
|
Play - The circular vertical section of the fixed track shown is smooth with ...
11:31
|
Play - The end 'A' of a uniform rod AB of length 'l' touches a horizontal smo...
06:30
|
Play - A man is standing on a cart of mass double the mass of man. Initially ...
02:55
|
Play