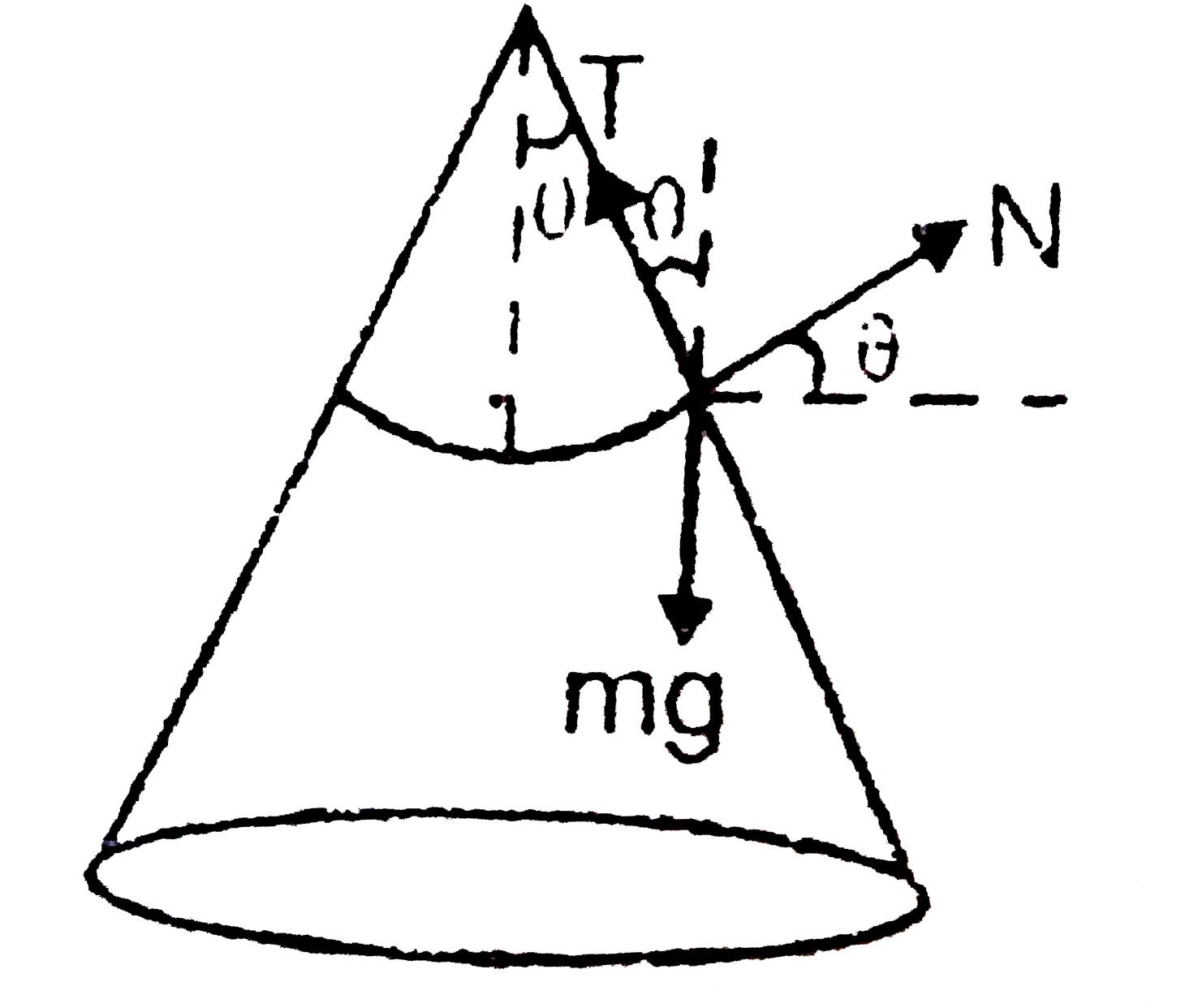A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.29|20 VideosView PlaylistDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.30|9 VideosView PlaylistDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.27|20 VideosView PlaylistCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 VideosView PlaylistELECTRO MAGNETIC WAVES
RESONANCE ENGLISH|Exercise Exercise 3|27 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.28
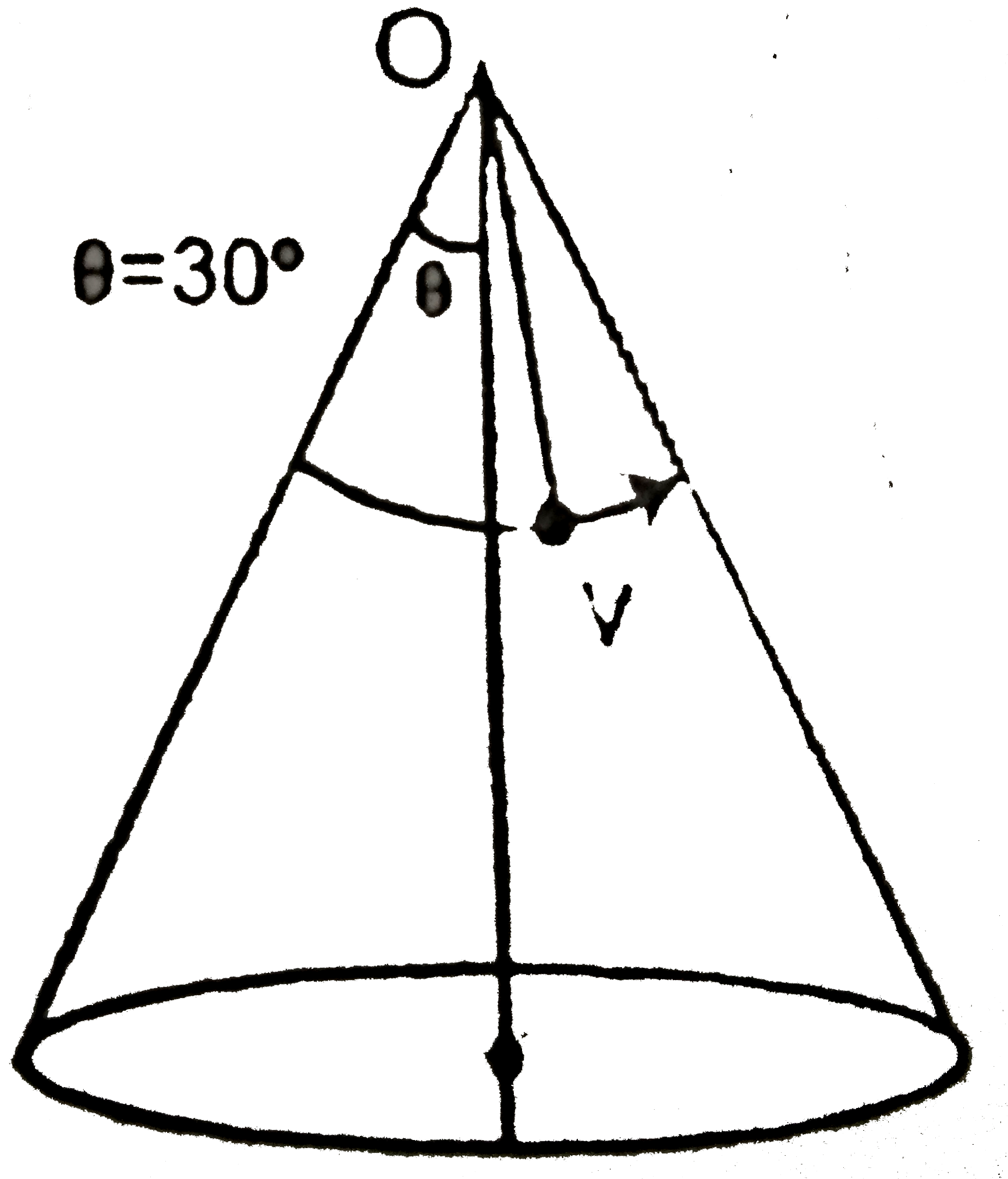
- A bob of mass 2kg is suspended from point O of a core with an inextens...
06:37
|
Playing Now - Block A is kept on block B as shown in figure. It is known that accele...
02:20
|
Play - Two point charges are placed in vacuum. It is observed that electrosta...
02:19
|
Play - A 20 gm particle is subjected to two simple harmonic motions x(1)=2 ...
02:46
|
Play - Two infinitely long line charges having charge density lamda each are ...
03:06
|
Play - A cyclist rides along the circumference of a circular horizontal plane...
02:40
|
Play - Scientists are working hard to develop nuclear fusion reactor Nuclei o...
02:48
|
Play - Assume that two deuteron nuclei in the core of fusion reactor at tempe...
02:46
|
Play - Result of calculations for four different design of a fusion reactor u...
01:38
|
Play