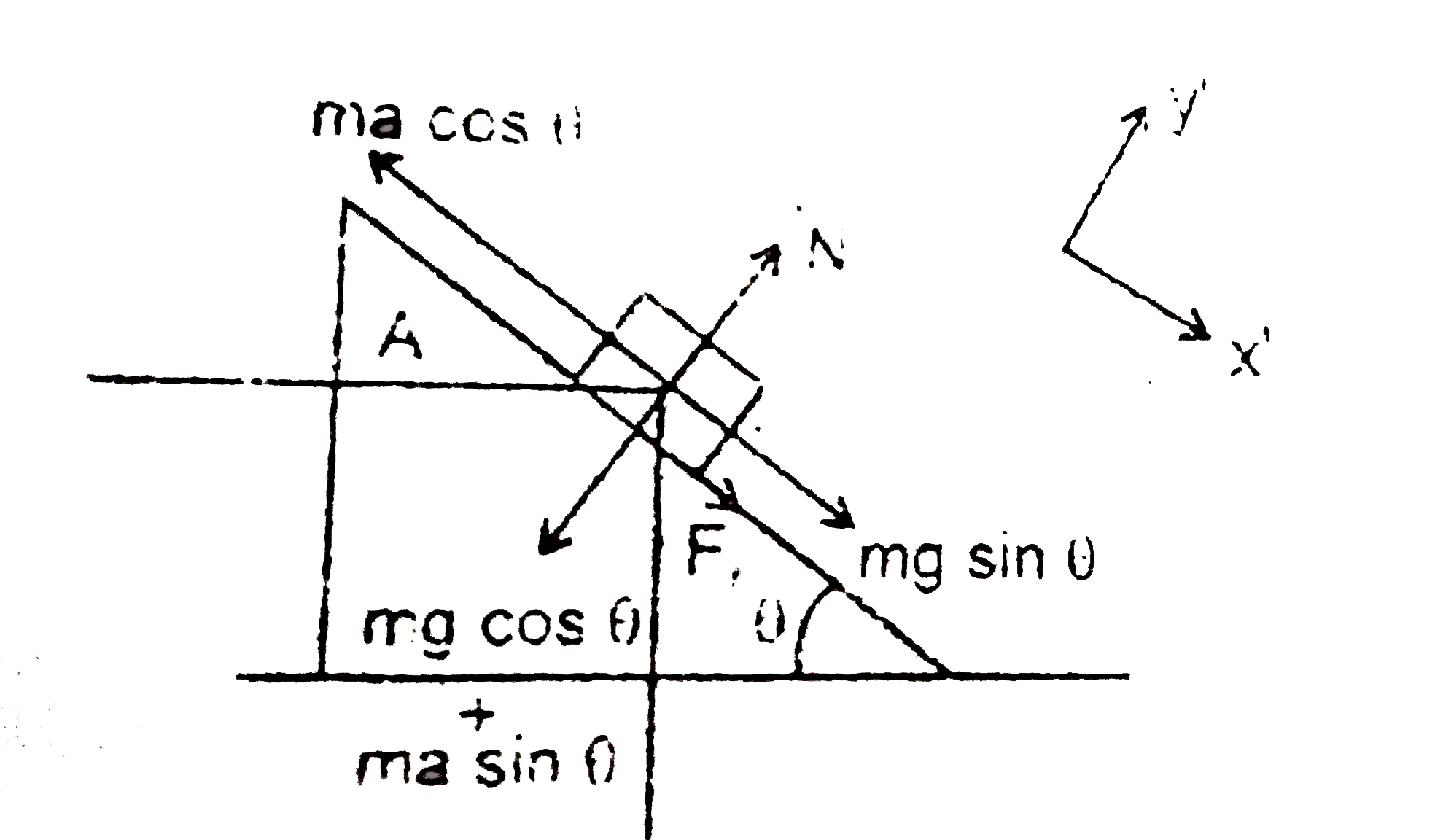A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.30|9 VideosView PlaylistDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.31|20 VideosView PlaylistDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.28|9 VideosView PlaylistCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 VideosView PlaylistELECTRO MAGNETIC WAVES
RESONANCE ENGLISH|Exercise Exercise 3|27 VideosView Playlist
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.29
- If the coefficient of friction between A and B is mu, the maximum acce...
03:08
|
Playing Now - The force acting on a particle moving along a straight line varies wit...
01:08
|
Play - A moving particle is acted upon by several forces F(1),F(2),F(3)….etc....
03:05
|
Play - A table fan, rotating at a speed of 2400 rpm, is switched off and the ...
02:34
|
Play - Graphs shows the acceleration of a 3 kg particle as an applied force m...
01:21
|
Play - Inside a horizontal moving box, an experimenter finds that when an obj...
01:54
|
Play - A man is supplying a constant power of 500 J//s to a massless string b...
03:57
|
Play - A trolley is being up an incline plane by a man inside the trolley He ...
02:20
|
Play - A motor is fixed inside a box which is moving upwards with velocity 5 ...
02:25
|
Play - A block A is kept on a rough inclined plane. Initially theta = 0. The ...
02:16
|
Play - The graph in the figure shows how the displacement of a particle descr...
04:28
|
Play - Two blocks of masses 6 kg and 3 kg are attached to the two ends of a m...
02:02
|
Play - An orbital electron in the ground state of hydrogen has an angular mom...
01:37
|
Play - The frequencies of x-rays, gamma rays and ultra-violet rays are respec...
01:57
|
Play - A person with a defective sight is using a lens having a power of +2D....
01:06
|
Play - During a negative beta decay.
01:50
|
Play - Two charges q(1) and q(2) are placed 30 cm apart, as shown in figure. ...
04:37
|
Play - The electric potential at a point in free space due to a charge Q coul...
02:15
|
Play - A metallic sphere floats in an immiscible mixture of water (rho(w)=10^...
01:53
|
Play - In an alpha -decay, the kinetic energy of alpha-particles is 48 MeV a...
02:49
|
Play