A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
TEST PAPERS
RESONANCE ENGLISH|Exercise PART - II PHYSICS|106 VideosView PlaylistSIMPLE HARMONIC MOTION
RESONANCE ENGLISH|Exercise Advanced Level Problems|13 VideosView PlaylistTEST SERIES
RESONANCE ENGLISH|Exercise PHYSICS|130 VideosView Playlist
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-TEST PAPERS-PHYSICS
- A pulley is attached to one arm of a balance and a string passed aroun...
04:29
|
Play - A parallel plate capacitor (without dielectric) is charged by a batter...
02:59
|
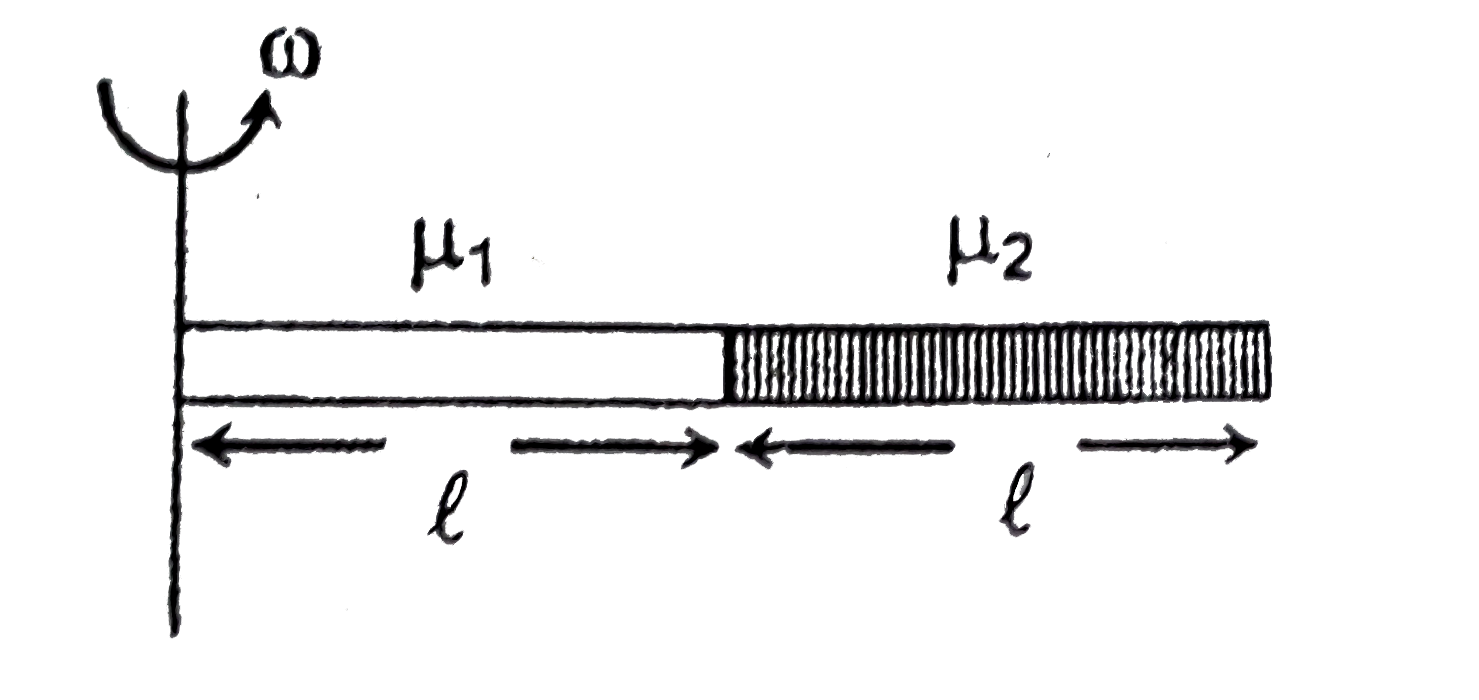
Play - Two thin rods of same length l but of different uniform mass per unit ...
02:42
|
Playing Now - In the given circuit, the valuue of R so that thermal power generated ...
01:56
|
Play - A closed organ pipe of length l is vibrating in its first overtone. Th...
05:39
|
Play - Shows an arrangement of identical metal plates paraed parallel to each...
04:57
|
Play - A cylinder is filled with a liquid of refractive index mu. The radius ...
05:30
|
Play - A point charge q is placed inside a conducting spherical shell of inne...
03:28
|
Play - A resistance of 4Omega and a wire of length 5 m and resistance 5Omega ...
02:55
|
Play - A satellite is launched into a circular orbit of radius R around earth...
03:53
|
Play - The pitch of a screw gauge is 1 mm and there are 100 division on its c...
02:45
|
Play - A copper rod and a steel rod of equal cross -sections and lengths (L) ...
03:26
|
Play - The left plate of the capacitor shown in the figure carries a charge +...
01:59
|
Play - A ray of light falls normally on one face of a right angled prims of r...
05:00
|
Play - The work done an a particle of mass m by a force K[(x)/((x^(2) + y^(...
03:45
|
Play - In the given situation, for what value of i, the incidence ray will re...
05:24
|
Play - A circuit is shown below.
05:23
|
Play - In the circuit, V is potential differences across the terminal as shwo...
02:24
|
Play - Find the ratio of charges on 5muF and 10muF capacitor when circuit is ...
03:16
|
Play - There exist magnetic field vec(B)=yhat(i)-xhat(j) in space. What is cu...
03:00
|
Play