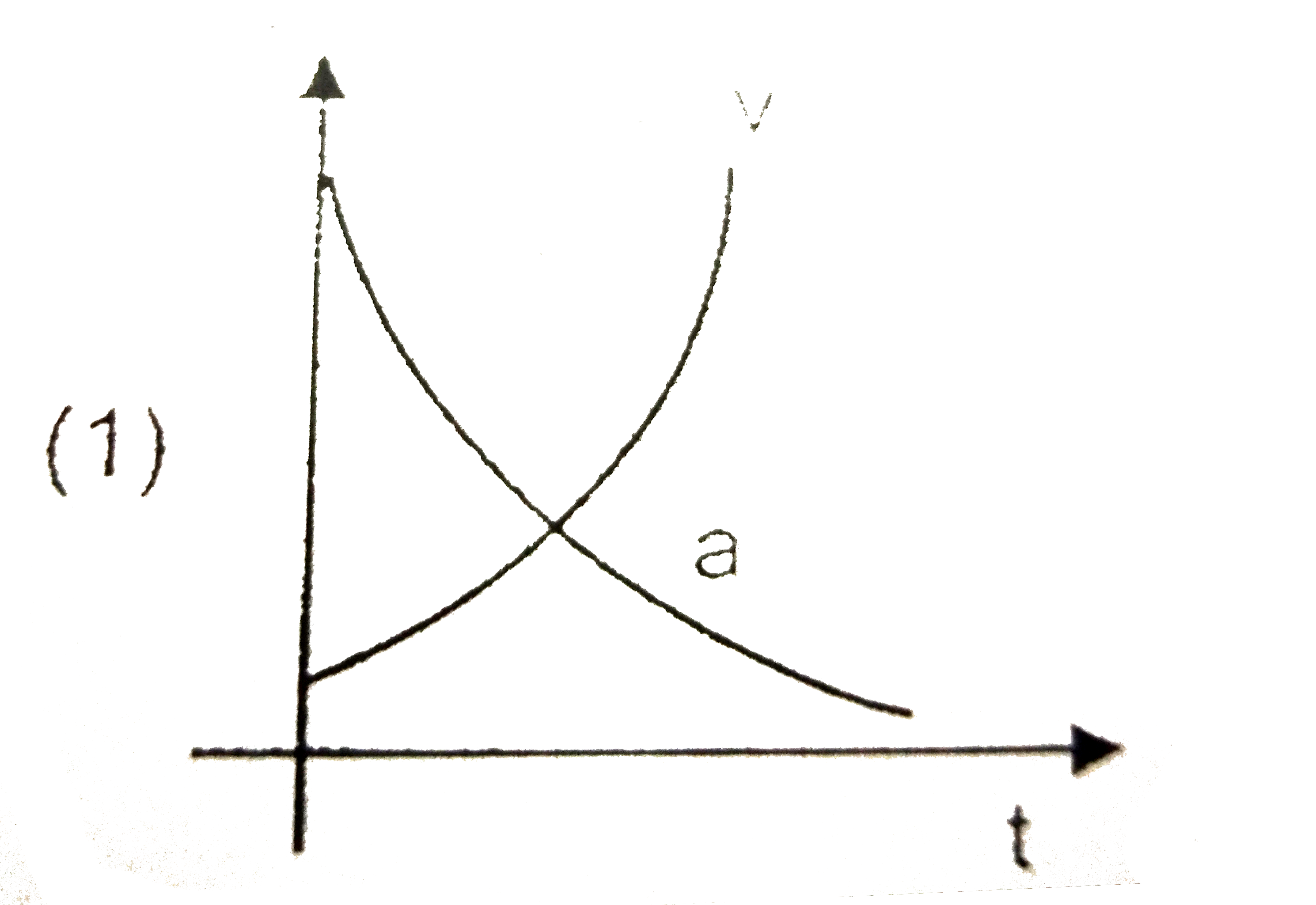
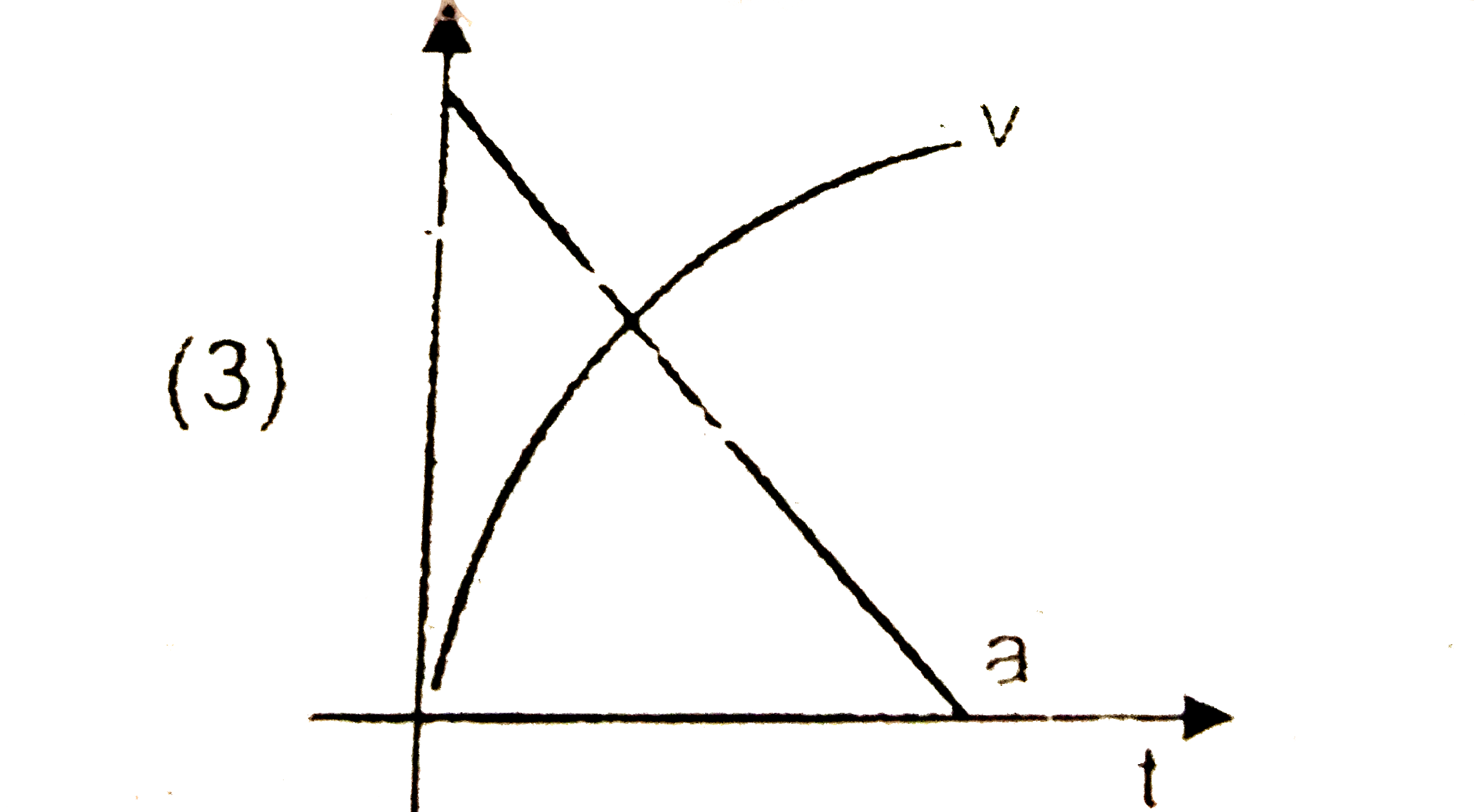
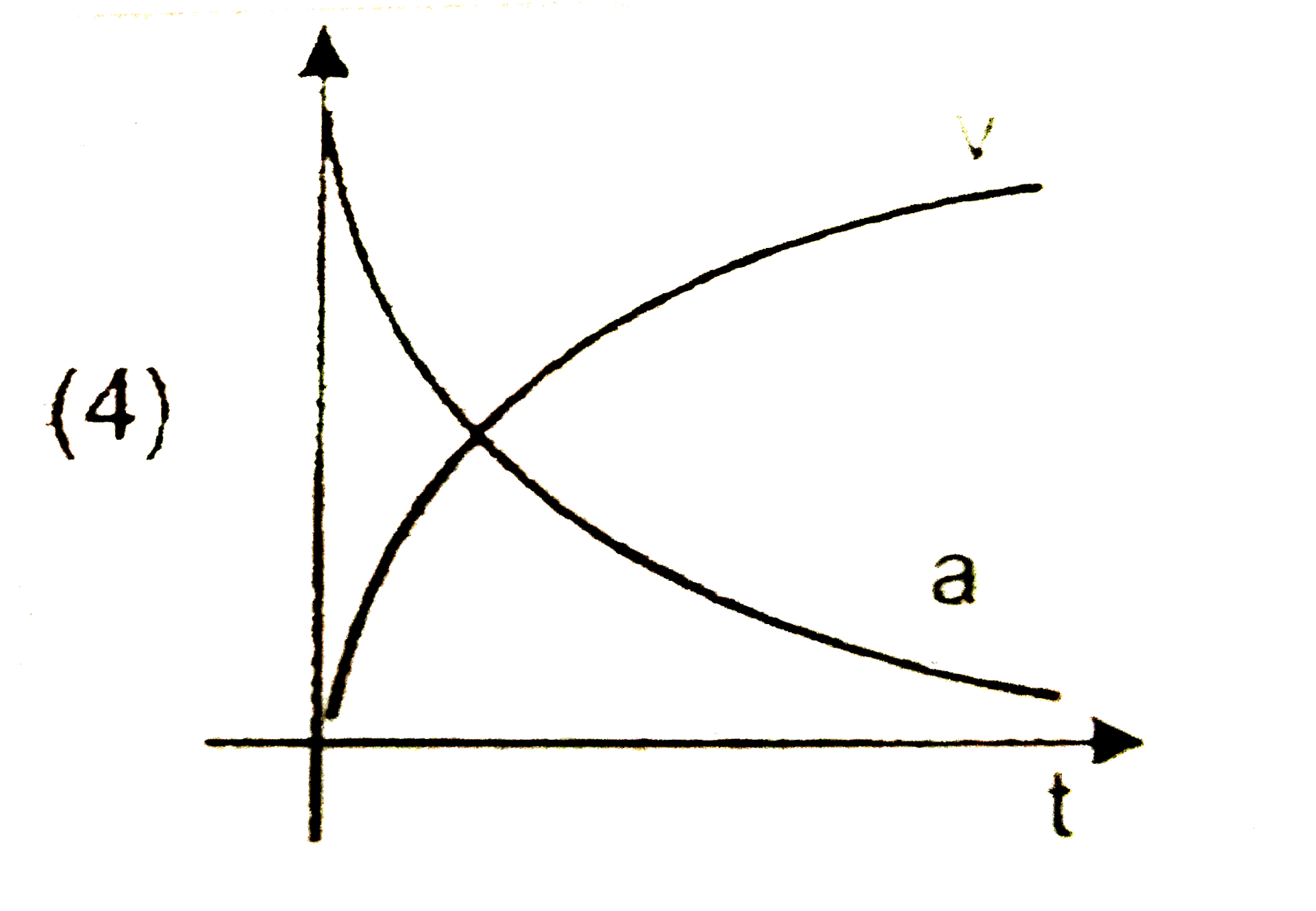
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
TEST PAPERS
RESONANCE ENGLISH|Exercise PART - II PHYSICS|106 VideosView PlaylistSIMPLE HARMONIC MOTION
RESONANCE ENGLISH|Exercise Advanced Level Problems|13 VideosView PlaylistTEST SERIES
RESONANCE ENGLISH|Exercise PHYSICS|130 VideosView Playlist
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-TEST PAPERS-PHYSICS
- An unknown transistor needs to be identified as npn and pnp type. A mu...
02:18
|
Play - A uniformly tapering conical wire is made from a material of young's m...
10:29
|
Play - Which of the following option correctly describes the variation of the...
02:52
|
Playing Now - An audio signal consists of two distinct sound. One a human speech sig...
02:46
|
Play - An electron in a hydrogen atom makes a transition from n = 2 to n = 1 ...
02:24
|
Play - When photons of wavlength lambda(1) are incident on an isolated sphere...
03:37
|
Play - In the following 'I' refers to current and other symbols have their us...
03:13
|
Play - If it takes 5 minutes to fill a 15 litre bucket from a water tap diame...
04:51
|
Play - x and y displacements of a particle are given as x(t)=-asinomegat and ...
02:07
|
Play - Suppose the drift velocity v(d) in a material varied with the applie...
02:08
|
Play - When the current in a coil changes from 5A to 2A in 0.1s, an average v...
02:01
|
Play - A 25 cm long solenoid has radius 2 cm and 500 total number of turns. I...
03:33
|
Play - You are asked to design a shaving mirror assuming that a person keeps ...
02:16
|
Play - If two glass plates have water between them and are separated by very ...
01:58
|
Play - In the circuit shown, charge on the capacitor connected between B and ...
03:06
|
Play - A 10kg weight is suspended with a wire AB of linear mass density 0.01k...
06:11
|
Play - A particle is moving in x-y plane with y=x/2 and v(x)=4-2t. The displa...
02:39
|
Play - Difference between nth and (n+1) the Bohr's radius of 'H' atom is equa...
02:07
|
Play - A radioactive substance X decays into another radioactive substance Y ...
02:20
|
Play - A charged particle enters a unifrom magnetic field with velocity vec...
01:47
|
Play