Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-JEE MAIN REVISION TEST -17 (2020)-PHYSICS
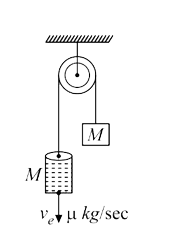
- Velocity of water flow in downward direction relative to cylindrical t...
Text Solution
|
- The density of water at the surface of the ocean is rho and atmospheri...
Text Solution
|
- A block of mass m is placed on an inclined plane with angle of inclina...
Text Solution
|
- The de-Broglie wavelength of an electron is same as the wavelength of ...
Text Solution
|
- Moseley's law for characteristic X-rays is sqrt v = a(Z-b). In this,
Text Solution
|
- In the figure shown a charge q moving with a velocity v along the x-a...
Text Solution
|
- Capacity of an isolated sphere is increased n times when it is enclose...
Text Solution
|
- Two non-conducting infinite plane sheets having charges distributed on...
Text Solution
|
- A rod of length L lies along the x-axis with its left end at the origi...
Text Solution
|
- In the following circuit a 10 m long potentiometer wire with resistanc...
Text Solution
|
- If E and B represent electric and magnetic field vectors of the electr...
Text Solution
|
- In a single slit diffraction experiment first minima for lambda1 = 660...
Text Solution
|
- A semi cylindrical shell with negligible thickness oscillates without ...
Text Solution
|
- The S-shaped unifrom wire shown in figure has a mass M, and the radius...
Text Solution
|
- The unit vectors hati, hatj and hatk are as shown below. What will be ...
Text Solution
|
- While measuring length of an object it was observed that the zero of t...
Text Solution
|
- A given LCR series circuit satisfes the condition for resonance with a...
Text Solution
|
- A ball is thrown vertically upwards. Which of the following plots repr...
Text Solution
|
- A thermodynamic process is shown in Fig. The pressures and volumes cor...
Text Solution
|
- The period of a satellite in a circular orbit of radius R is T. What i...
Text Solution
|