Home
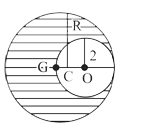
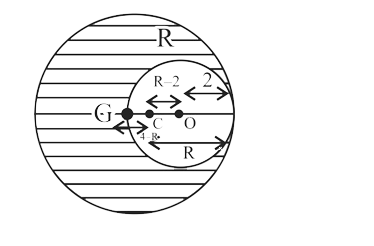
Class 12
PHYSICS
As shown in figure, when a spherical cav...

As shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:

A

`(R^2 - 2 R+4)(4-R)=8`

B

`(R^2 + 2R-4)(4-R)=8`

C

`(R^2 + 2 R+4)(4-4)=8`

D

`(R^2-2 R-4)(4-R)=8`

Text Solution

Verified by Experts

The correct Answer is:
C
By concept of COM
`m_1 R_1 = m_2R_2`
Remaining mass `xx` (4-R) = Cavity mass `xx`(R-2)
`(4/3piR^2 rho-4/3 pi2^3 rho)(4-R)=4/3 pi2^3 rho xx(Rxx2)`
`(R^2 + 2R+4)(4-R)=8`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • JEE MAIN REVISION TEST - 27 - JEE -2020

    VMC MODULES ENGLISH|Exercise PHYSICS (SECTION 2)|5 Videos

  • JEE MAIN REVISION TEST - 26 (2020)

    VMC MODULES ENGLISH|Exercise PHYSICS (SECTION 2)|5 Videos

  • JEE MAIN REVISION TEST - 28

    VMC MODULES ENGLISH|Exercise PHYSICS (SECTION-2)|5 Videos

Similar Questions

Explore conceptually related problems

A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

A uniform metal disck of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be

From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)

From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)

A spherical cave of radius R/2 was carved out from a uniform sphere of radius R and original mass M. the center of the cave is at R/2 from the center of the large sphere. Point P is at a distance 2R from the center the large sphere and on the joing line of the two centers. the gravitational field strength g at point P is

A hemi-spherical cavity is created in solid sphere (of radius 2R ) as shown in the figure. Then

A semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is

The radius of gyration of a uniform solid sphere of radius R., about an axis passing through a point R/2 away from the centre of the sphere is:

Home
Profile