Home
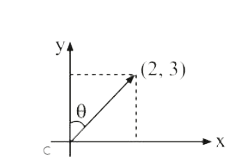
Class 12
PHYSICS
Given vectoroverset(rarr)A=2 hat I +3hat...

Given vector`overset(rarr)A=2 hat I +3hatj` , the angle between `overset(rarr)A` and y-axis is :

A

`tan^(-1)3//2`

B

`tan^(-1) 2//32`

C

`sin^(-1)2//3`

D

`cos^(-1)2//3`

Text Solution

Verified by Experts

The correct Answer is:
b
`tan theta =2/3`
`theta =-tan^(-1)2/3`
Promotional Banner

Topper's Solved these Questions

  • INTRODUCTION TO VECTORS & FORCES

    VMC MODULES ENGLISH|Exercise level 2|65 Videos

  • INTRODUCTION TO VECTORS & FORCES

    VMC MODULES ENGLISH|Exercise JEE Main ( ARCHIVE ) ( LEVEL-1)|12 Videos

  • INTRODUCTION TO VECTORS & FORCES

    VMC MODULES ENGLISH|Exercise JEE Advanced ( ARCHIVE LEVEL-2)|12 Videos

  • GRAVITATION

    VMC MODULES ENGLISH|Exercise JEE Advance (Archive) TRUE/FALSE|1 Videos

  • JEE MAIN - 5

    VMC MODULES ENGLISH|Exercise PART I : PHYSICS (SECTION - 2)|5 Videos

Similar Questions

Explore conceptually related problems

Dot product of two vectors overset(rarr)A and overset(rarr)B is defined as overset(rarr)A.overset(rarr)B=aB cos phi , where phi is angle between them when they are drawn with tails coinciding. For any two vectors . This means overset(rarr)A . overset(rarr)B=overset(rarr)B. overset(rarr)A that . The scalar product obeys the commutative law of multiplication, the order of the two vectors does not matter. The vector product of two vectors overset(rarr)A and overset(rarr)B also called the cross product, is denoted by overset(rarr)A xx overset(rarr)B . As the name suggests, the vector product is itself a vector. overset(rarr)C=overset(rarr)A xx overset(rarr)B then C=AB sin theta , overset(rarr)A=hat i+ hat j-hatk and overset(rarr)B=2 hat i +3 hat j +5 hat k angle between overset(rarr)A and overset(rarr)B is

If overset(rarr)A+overset(rarr)B+overset(rarr)C =0 and A = B + C, the angle between overset(rarr)A and overset(rarr)B is :

The area of parallelogram represented by the vectors overset(rarr)A = 2 hat i + 3 hat j and overset(rarr)B=hat i+4 hat j is

The maqunitudes of vecotr overset(rarrA), overset(rarr)B and overset(rarr)C are respectively 12,5 and 13 units and overset(rarr)A+overset(rarr)B=overset(rarr)C then the angle between overset(rarr)A and overset(rarr)B is :

What is the projection of vector overset(rarr)A=4hat I +3 hatj on vector overset(rarr)B=3hat I +4 hat j ?

Find unit vectors along overset(rarr)A=hat I + hat j - 2 hat k and overset(rarr)B=hat I +2 hat j -hat k

If |overset(rarr)A+overset(rarr)B|=|overset(rarr)A-overset(rarr)B| what is the angle between overset(rarr)A and overset(rarr)B ?

If |overset(rarr)A-overset(rarr)B|=|overset(rarr)A|-|overset(rarr)B| the angle between overset(rarr)A and overset(rarr)B is

If overset(rarr)A=overset(rarr)B+overset(rarr)C and the magnitude of overset(rarr)A, overset(rarr)B and overset(rarr)C are 5,4 and 3 units respectively the angle between overset(rarr)A and overset(rarr)C is

Let overset(to)(a) =a_(1) hat(i) + a_(2) hat(j) + a_(3) hat(k) , overset(to)(b) = b_(1) hat(i) +b_(2) hat(j) +b_(3) hat(k) " and " overset(to)(c) = c_(1) hat(i) +c_(2) hat(j) + c_(3) hat(k) be three non- zero vectors such that overset(to)(c ) is a unit vectors perpendicular to both the vectors overset(to)(a ) and overset(to)(b) . If the angle between overset(to)(a) " and " overset(to)(b) is (pi)/(6) then |{:(a_(1),,a_(2),,a_(3)),(b_(1),,b_(2),,b_(3)),(c_(1),,c_(2),,c_(3)):}|^2 is equal to

VMC MODULES ENGLISH-INTRODUCTION TO VECTORS & FORCES -level 1
  1. A car is moving on horizontal ground with a velocity vm s^(-1) with ...

    Text Solution

    |

  2. An aeroplane pilot wishes to fly due west A wind of 100 km h^-1 is blo...

    Text Solution

    |

  3. A train 100 m long travelling at 40 ms^(-1) starts overtaking another ...

    Text Solution

    |

  4. The diagram shows a train moving with constant velocity and a car movi...

    Text Solution

    |

  5. A bird is flying towards north with a velocity 40 km h^-1 and a train ...

    Text Solution

    |

  6. Given vectoroverset(rarr)A=2 hat I +3hatj , the angle between overset...

    Text Solution

    |

  7. If the vectors 2 hati +3 hat j +chatj and -3hat i+6hatk are orthogo...

    Text Solution

    |

  8. Consider a F = 4hati -3hatj . Another vector perpendicular to F is

    Text Solution

    |

  9. The angle between the two vector -2hati+3hatj+hatk and hati+2hatj-4hat...

    Text Solution

    |

  10. For any two vectors barA and barB if barA.barB=|bar AxxbarB|, the ma...

    Text Solution

    |

  11. The angle between vector (overset(rarr)Axxoverset(rarr)B) and (overset...

    Text Solution

    |

  12. what is the angle between (overset(rarr)P+overset(rarr)Q) and (overset...

    Text Solution

    |

  13. Which of the following is the unit vector perrpendicular to A and B?

    Text Solution

    |

  14. A vector A points vertically upward and B points towards north.The vec...

    Text Solution

    |

  15. Two vectors P=2hat I +bhat j +2hat k and Q=hat i+hat j+hat k will be ...

    Text Solution

    |

  16. What is the unit vector perpendicular to the following Vector 2hat(i)+...

    Text Solution

    |

  17. The magnitude of the vector product of two vectors is sqrt(3) times th...

    Text Solution

    |

  18. A and B are two vectors in a plane at an angle of 60^(@) with each oth...

    Text Solution

    |

  19. Projection of overset(rarr)P on overset(rarr)Q is :

    Text Solution

    |

  20. What is the projection of vector overset(rarr)A=4hat I +3 hatj on vec...

    Text Solution

    |