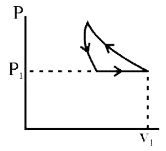
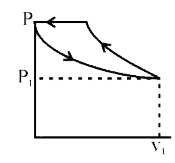
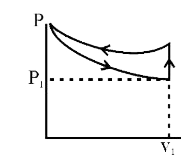
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
GASEOUS STATE & THERMODYNAMICS
VMC MODULES ENGLISH|Exercise JEE MAIN (ARCHIVE )|81 VideosView PlaylistGASEOUS STATE & THERMODYNAMICS
VMC MODULES ENGLISH|Exercise JEE ADVANCED (ARCHIVE )|111 VideosView PlaylistGASEOUS STATE & THERMODYNAMICS
VMC MODULES ENGLISH|Exercise Level - 1|75 VideosView PlaylistENERGY & MOMENTUM
VMC MODULES ENGLISH|Exercise JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE|1 VideosView PlaylistGRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive) TRUE/FALSE|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-GASEOUS STATE & THERMODYNAMICS-Level - 2
- Two gases have the same initial pressure, volume and temperature. They...
06:59
|
Play - The volume of air increases by 10% in the adiabatic expansion. The app...
02:57
|
Play - Choose the correct option: In the arrangement shown in Fig. gas is t...
04:14
|
Play - Match the column I with column II.
00:50
|
Play - An ideal gas is kept in two adjacent chambers of volume V and 2V, sepa...
05:08
|
Play - 3 mole of an ideal gas is taken through the process shown. BC is adiab...
05:31
|
Play - One mole of an ideal gas undergoes a process T = 300 + 2V. Then amount...
03:49
|
Play - One mole of an ideal gas whose adiabatic exponent is gamma = 4/3 unde...
03:21
|
Play - Find the amount of work done to increase the temperature of one mole j...
03:30
|
Play - A certain mass of an ideal gas is at pressure P(1) and volume V(1). If...
05:55
|
Playing Now - Cp is always greater than Cv for a gas, which of the following stateme...
03:29
|
Play - A system undergoes a cyclic process in which it absorbs Q(1) heat and ...
02:40
|
Play - An ideal gas of mass m in a state A goes to another state B Vialpha th...
01:09
|
Play - Two mole of Hydrogen and three mole of Helium are mixed at room temper...
06:16
|
Play - For a gas, molar specific heat in a process is greater then CV . Which...
01:53
|
Play - One mole of a monoatomic ideal gas undergoes the process ArarrB in the...
06:54
|
Play - Molar heat capacity of gas whose molar heat capacity at constant volum...
04:48
|
Play - A container of volume 4V(0) made of a perfectly non- conducting materi...
08:57
|
Play - A container of volume 4V(0) made of a perfectly non- conducting materi...
04:42
|
Play - A container of volume 4V(0) made of a perfectly non- conducting materi...
04:01
|
Play