Home
Class 9
MATHS
In Fig. 9.13, ABCD is a parallelogram an...

In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, `AL bot DC`. Prove that (i) ar (ABCD) = ar (EFCD) (ii) ar (ABCD) = DC × AL

Answer

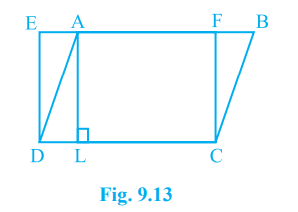
Step by step text solution for In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, AL bot DC. Prove that (i) ar (ABCD) = ar (EFCD) (ii) ar (ABCD) = DC × AL by MATHS experts to help you in doubts & scoring excellent marks in Class 9 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • AREAS OF PARALLELOGRAMS AND TRIANGLES

    PSEB|Exercise EXAMPLE|4 Videos

  • CIRCLES

    PSEB|Exercise EXAMPLE|6 Videos

Similar Questions

Explore conceptually related problems

In the given fig. ABCD is a parallelogram and ABE is a triangle. Also AB||CE . If ar (ABCD) = 60 cm^2 then ar (DeltaABE) is :

In the figure. ABCD is a parallelogram and O is any point on BC . Prove that ar (triangleABO) + ar (triangleDOC) = ar(triangleODA)

In Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:- (i) ar (ACB) = ar (ACF) (ii) ar (AEDF) = ar (ABCDE)

In a parallelogram ABCD, the bisector of /_A also bisects BC at X. Prove that AD = 2AB.

ABCD is parallelogram. X and Y are the mid-points of BC and CD respectively. Prove that ar (DeltaAXY) =3/8 ar (||)^(gm) ABCD .

ABCD is parallelogram. X and Y are the mid-points of BC and CD respectively. Prove that ar (DeltaAXY) =3/8 ar (||gm ABCD) .

In Fig. if parallelogram ABCD and rectangle ABEF are of equal area, then :

In Fig. If parallelogram ABCD and rectangle ABEF are of equal area, then :

Two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that ar(||gmABCD) + ar(||gmAEFB) = ar(||gm EFCD)

In Fig. ABCD is a parallelogram. Prove that ar (DeltaACP) = ar (DeltaDPQ) .

Home
Profile