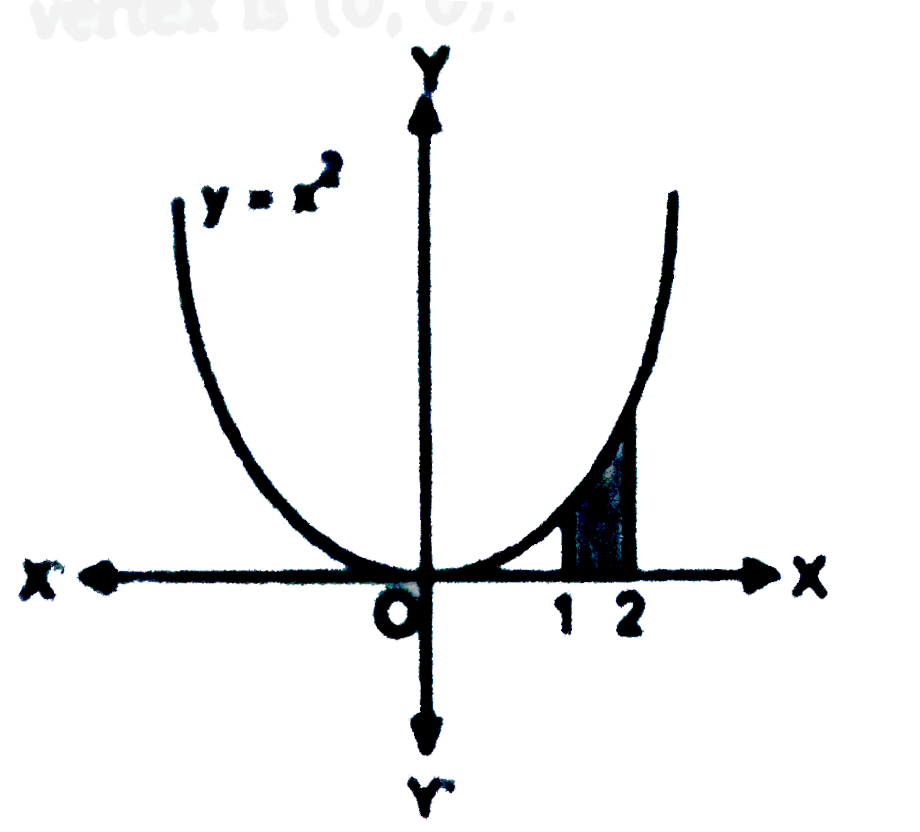Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF INTEGRALS-Miscellaneous Exercise
- Find the area under the given curves and given lines:(i) y=x^2,x = 1,...
Text Solution
|
- Find the area between the curves y = xand y=x^2.
Text Solution
|
- Find the area of the region lying in the first quadrant and bounded b...
Text Solution
|
- Sketch the graph y=|x+3|dot Evaluate int(-6)^0|x+3|dxdot What does the...
Text Solution
|
- Find the area between the x-axis and the curve y=sinx from x=0 to x=2p...
Text Solution
|
- Find the area of the region enclosed by the parabola y^2=4a x\ a n d t...
Text Solution
|
- Find the area enclosed by the parabola 4y=3x^2 and the line 2y=3x+12.
Text Solution
|
- Find the area of the smaller region bounded by the ellipse (x^2)/9+(y^...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse (x^2)/(a^2)...
Text Solution
|
- Find the area of the region enclosed by the parabola x^2=y , the li...
Text Solution
|
- Using the method of integration find the area bounded by the curve ...
Text Solution
|
- Find the area bounded by curves {(x ,y):ygeqx^2 and y = | x |}
Text Solution
|
- Using the method of integration find the area of the triangle ABC, ...
Text Solution
|
- Using the method of integration find the area of the region bounded b...
Text Solution
|
- Find the area of the region {(x , y): y^2lt=4x ,4x^2+4y^2lt=9}
Text Solution
|
- Area bounded by the curve y=x^3, the x-axis and the ordinates x = -2 ...
Text Solution
|
- The area bounded by the curve y=x |x|, x-axis and the ordinates x=-1 &...
Text Solution
|
- The area of the circle x^2+y^2=16exterior to the parabola y^2=6xis(A) ...
Text Solution
|
- Find the area bounded by the y-axis, y=cosx ,a n dy=sinxw h e n0lt=xlt...
Text Solution
|