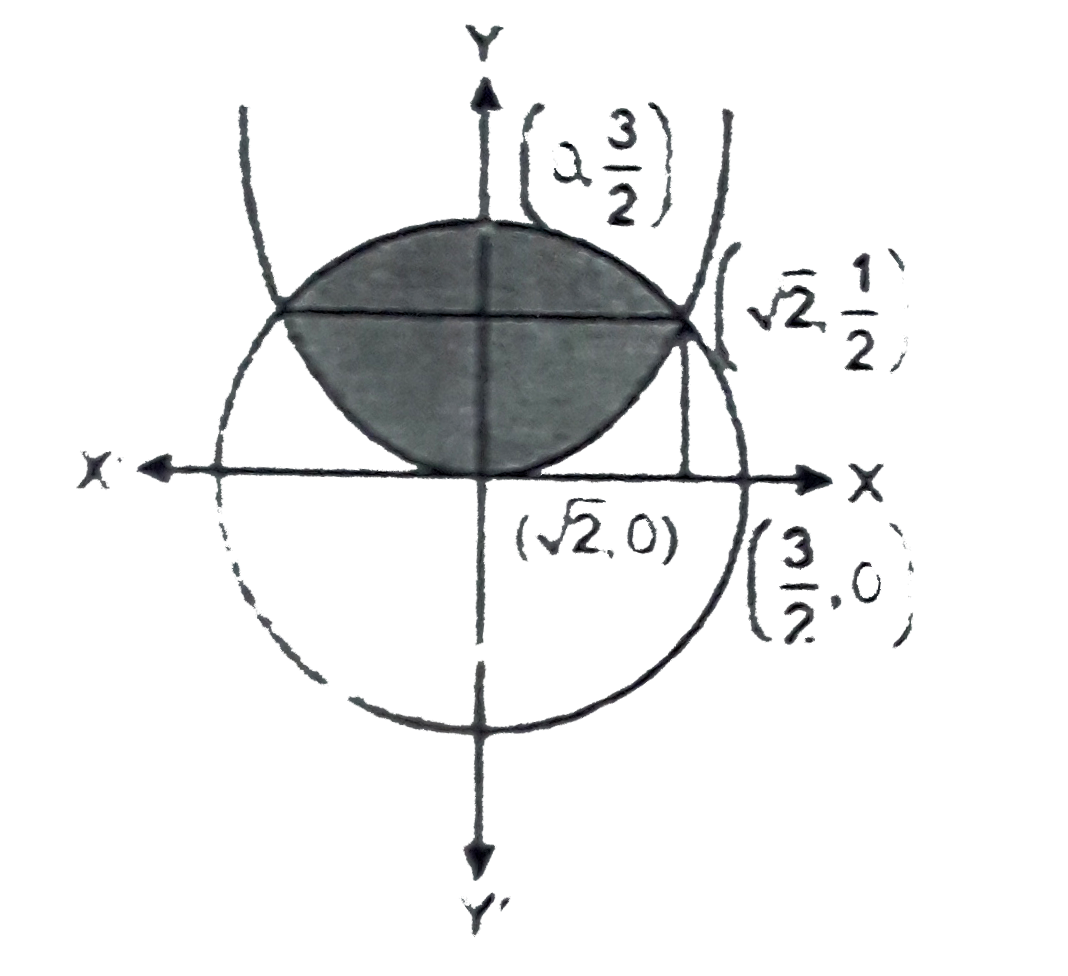Text Solution
Verified by Experts
Topper's Solved these Questions
APPLICATIONS OF INTEGRALS
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|19 VideosAPPLICATIONS OF INTEGRALS
NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 8.1|13 VideosAPPLICATIONS OF DERIVATIVES
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|24 VideosContinuity and Differentiability
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|23 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF INTEGRALS-Exercise 8.2
- Find the area of circle 4x^2+4y^2=9 which is interior to the parabo...
Text Solution
|
- Find the area bounded by curves (x-1)^2+y^2=1and x^2+y^2=1.
Text Solution
|
- Find the area of the region bounded by the curves y=x^2+2, y = x , x ...
Text Solution
|
- Find the area region bounded by the triangle whose vertices are (-1,1)...
Text Solution
|
- Using integration find the area of the triangular region whose side...
Text Solution
|
- Smaller area enclosed by the circle x^2+y^2=4 and the line x + y = 2 ...
Text Solution
|
- Area lying between the curves y^2=4x and y = 2x is:
Text Solution
|