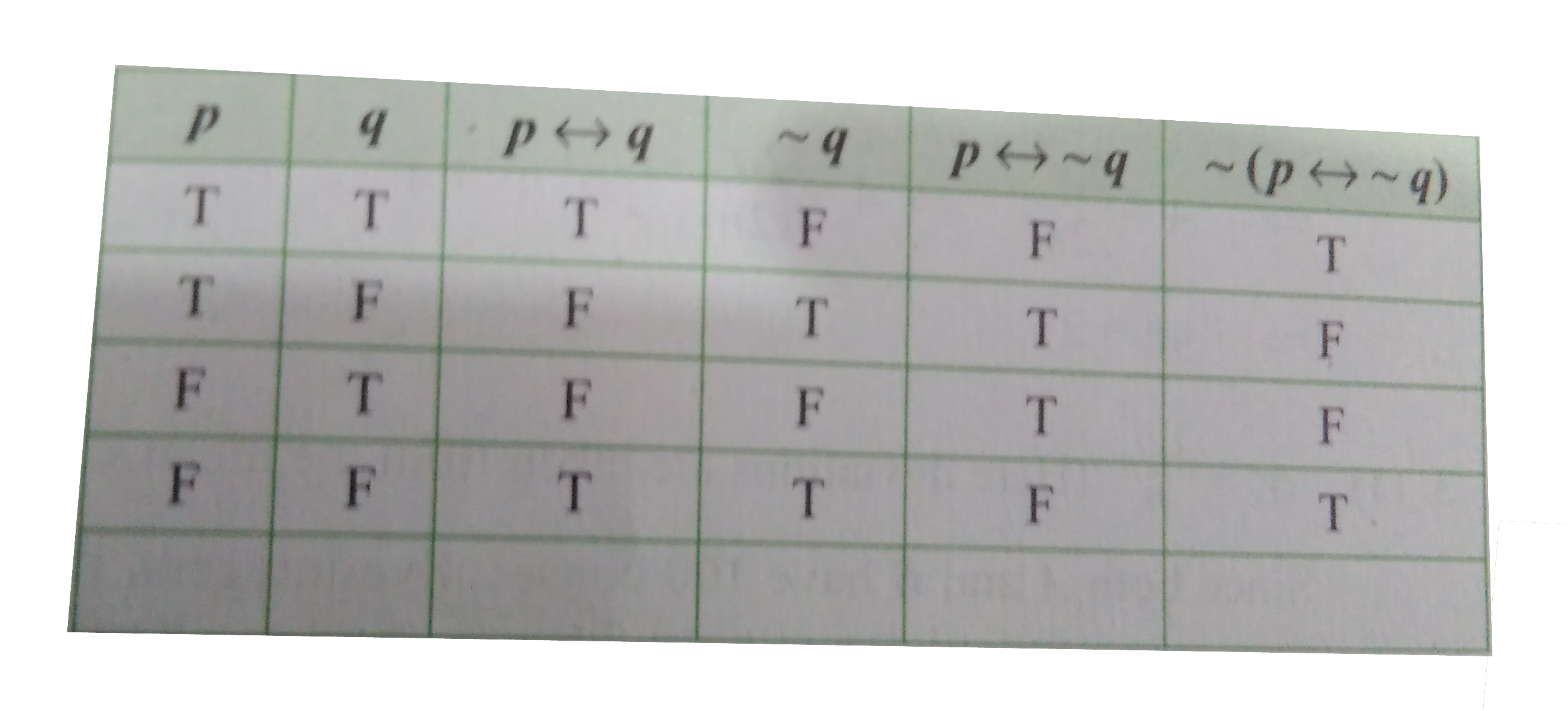A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-MATHMETICAL REASONING-JEE Previous Year
- Statement-1: ~(pharr~q) is equivalent to (pharrq). Statement-2: ~(p...
Text Solution
|
- Let S be a non-empty subset of R. consider the following statement: ...
Text Solution
|
- Consider the following statements p: Suman is brilliant q: Suman i...
Text Solution
|
- The negation of the statement "If I becomes a teacher, then I will o...
Text Solution
|
- Consider : Statement I: (p^^~q)^^(~p^^q) is a fallacy Statement ...
Text Solution
|
- The statement ~(pharr ~q) is
Text Solution
|
- The negation of ~svv(~r^^s) is equivalent to
Text Solution
|
- The Boolean Expression (p^^~ q)vvqvv(~ p^^q) is equivalent to :
Text Solution
|
- The following statement (p to q) to [(~p to q) to q] is
Text Solution
|
- The Boolean Expression ~(pvvq) vv(~pvvq) is equivalent to
Text Solution
|