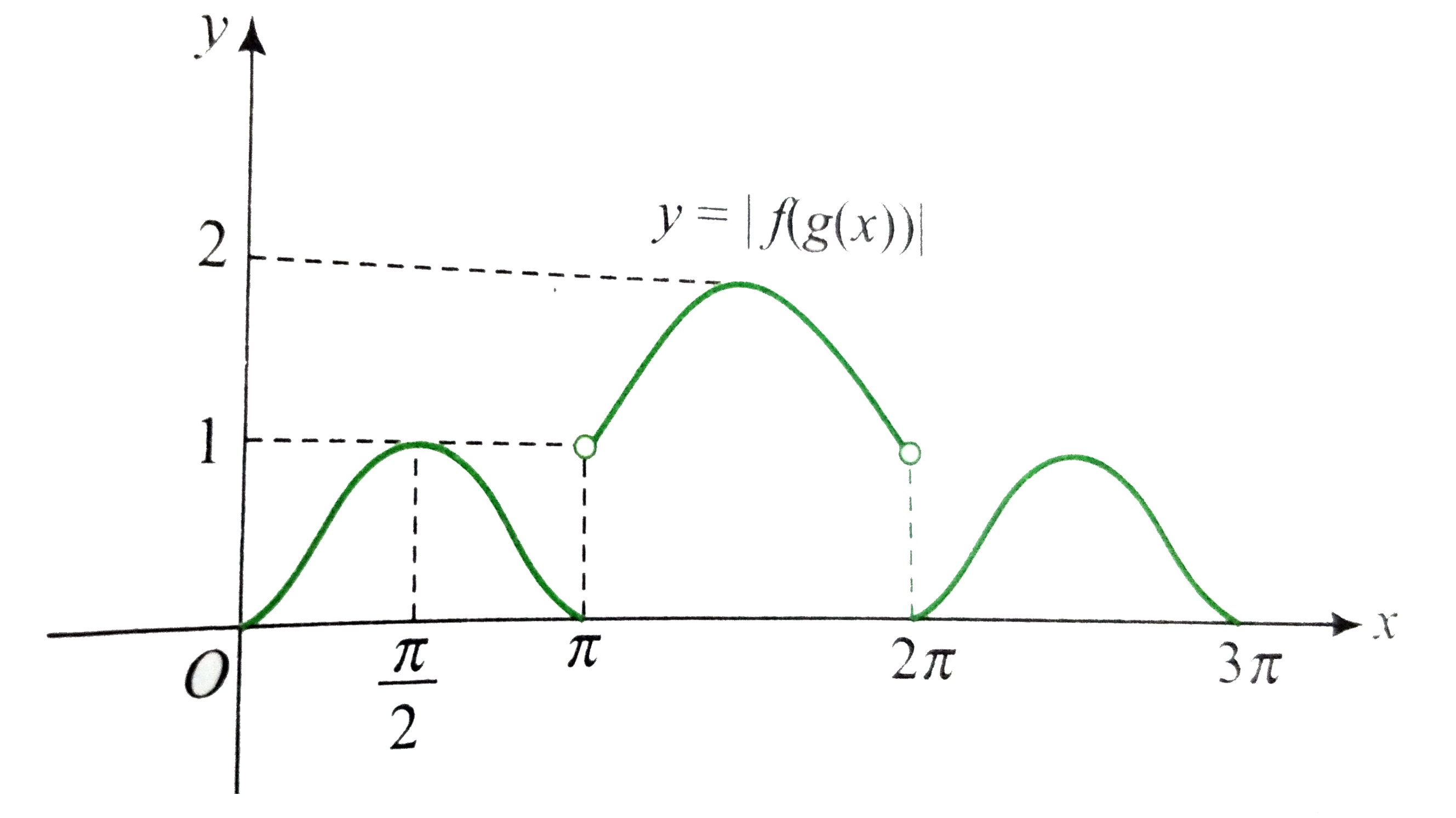
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
RELATIONS AND FUNCTIONS
CENGAGE|Exercise Exercise (Matrix)|9 VideosView PlaylistRELATIONS AND FUNCTIONS
CENGAGE|Exercise Exercise (Numerical)|31 VideosView PlaylistRELATIONS AND FUNCTIONS
CENGAGE|Exercise Exercise (Multiple)|27 VideosView PlaylistQuadratic Equations, Inequalities, Modulus and Logarithms
CENGAGE|Exercise Question Bank|28 VideosView PlaylistSCALER TRIPLE PRODUCTS
CENGAGE|Exercise DPP 2.3|11 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CENGAGE-RELATIONS AND FUNCTIONS-Exercise (Comprehension)
- If (f(x))^(2)xxf((1-x)/(1+x))=64x AAx in D(f), then The value of f...
07:44
|
Play - f(x)={(x-1",",-1 le x le 0),(x^(2)",",0le x le 1):} and g(x)=sinx ...
04:31
|
Play - f(x)={(x-1",",-1 le x le 0),(x^(2)",",0le x le 1):} and g(x)=sinx ...
05:54
|
Playing Now - f(x)={(x-1",",-1 le x le 0),(x^(2)",",0le x le 1):} and g(x)=sinx ...
05:42
|
Play - If a0 = x,a(n+1)= f(an), where n = 0, 1, 2, ..., then answer thefoll...
03:16
|
Play - If a(0)=x,a(n+1)=f(a(n)), " where " n=0,1,2, …, then answer the follow...
03:14
|
Play - If a(0)=x,a(n+1)=f(a(n)), " where " n=0,1,2, …, then answer the follow...
04:00
|
Play - Let f(x)=f1(x)-2f2 (x), where ,where f1(x)={((min{x^2,|x|},|x|le 1),(...
06:47
|
Play - Let f(x)=f(1)(x)-2f(2)(x), where where f(x)={(min{x^(2)","|x|}",",|x...
Text Solution
|
Play - Let f(x)=f(1)(x)-2f(2)(x), where where f(x)={(min{x^(2)","|x|}",",|x...
06:47
|
Play - Let f(x)={(2x+a",",x ge -1),(bx^(2)+3",",x lt -1):} and g(x)={(x+4",...
Text Solution
|
Play - Let f(x)={(2x+a",",x ge -1),(bx^(2)+3",",x lt -1):} and g(x)={(x+4",...
Text Solution
|
Play - Let f(x)={(2x+a",",x ge -1),(bx^(2)+3",",x lt -1):} and g(x)={(x+4",...
Text Solution
|
Play - Let f : R -> R is a function satisfying f(2-x) = f(2 + x) and f(20-x)...
03:13
|
Play - Let f:R to R be a function satisfying f(2-x)=f(2+x) and f(20-x)=f(x) ...
Text Solution
|
Play - Let f:R to R be a function satisfying f(2-x)=f(2+x) and f(20-x)=f(x) ...
03:28
|
Play - Consider two functions f(x)={([x]",",-2le x le -1),(|x|+1",",-1 lt x...
06:28
|
Play - Consider two functions f(x)={([x]",",-2le x le -1),(|x|+1",",-1 lt x...
06:28
|
Play - Consider two functions f(x)={([x]",",-2le x le -1),(|x|+1",",-1 lt x...
06:28
|
Play - Consider a function f whose domain is [-3, 4] and range is [-2, 2] wit...
04:30
|
Play