A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-ELLIPSE -Multiple Correct Answers Type
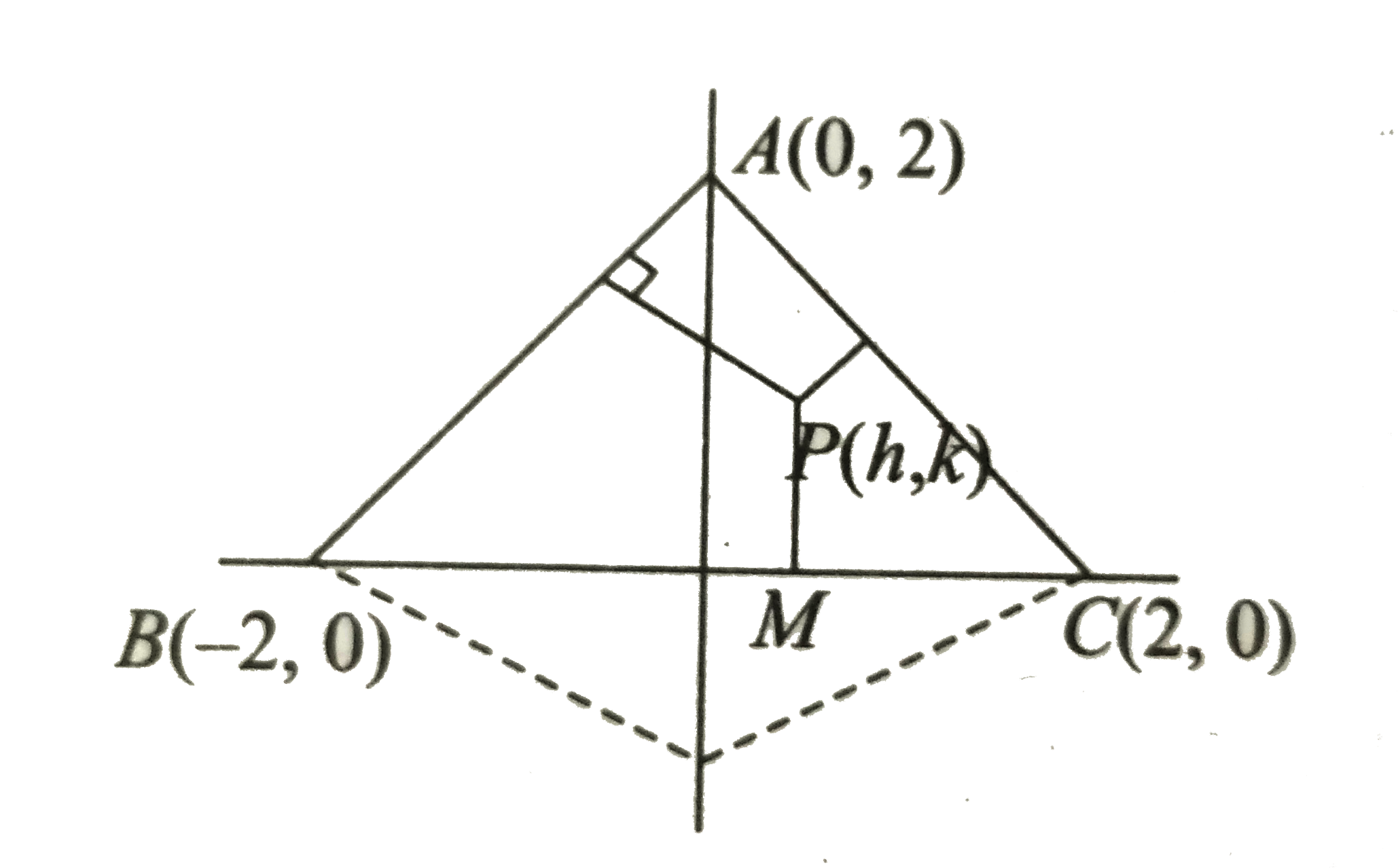
- In triangle ABC, a = 4 and b = c = 2 sqrt(2). A point P moves within t...
Text Solution
|
- Extremities of the latera recta of the ellipses (x^2)/(a^2)+(y^2)/(b^...
Text Solution
|
- Identify correct statement(s) about conic sqrt((x-5)^(2)+(y-7)^(2)) +...
Text Solution
|
- P and Q are two points on the ellipse (x^(2))/(a^(2)) +(y^(2))/(b^(2))...
Text Solution
|
- For the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)) =1 and (x^(2))/(b^(2))...
Text Solution
|
- AB and CD are two equal and parallel chords of the ellipse (x^(2))/(a^...
Text Solution
|