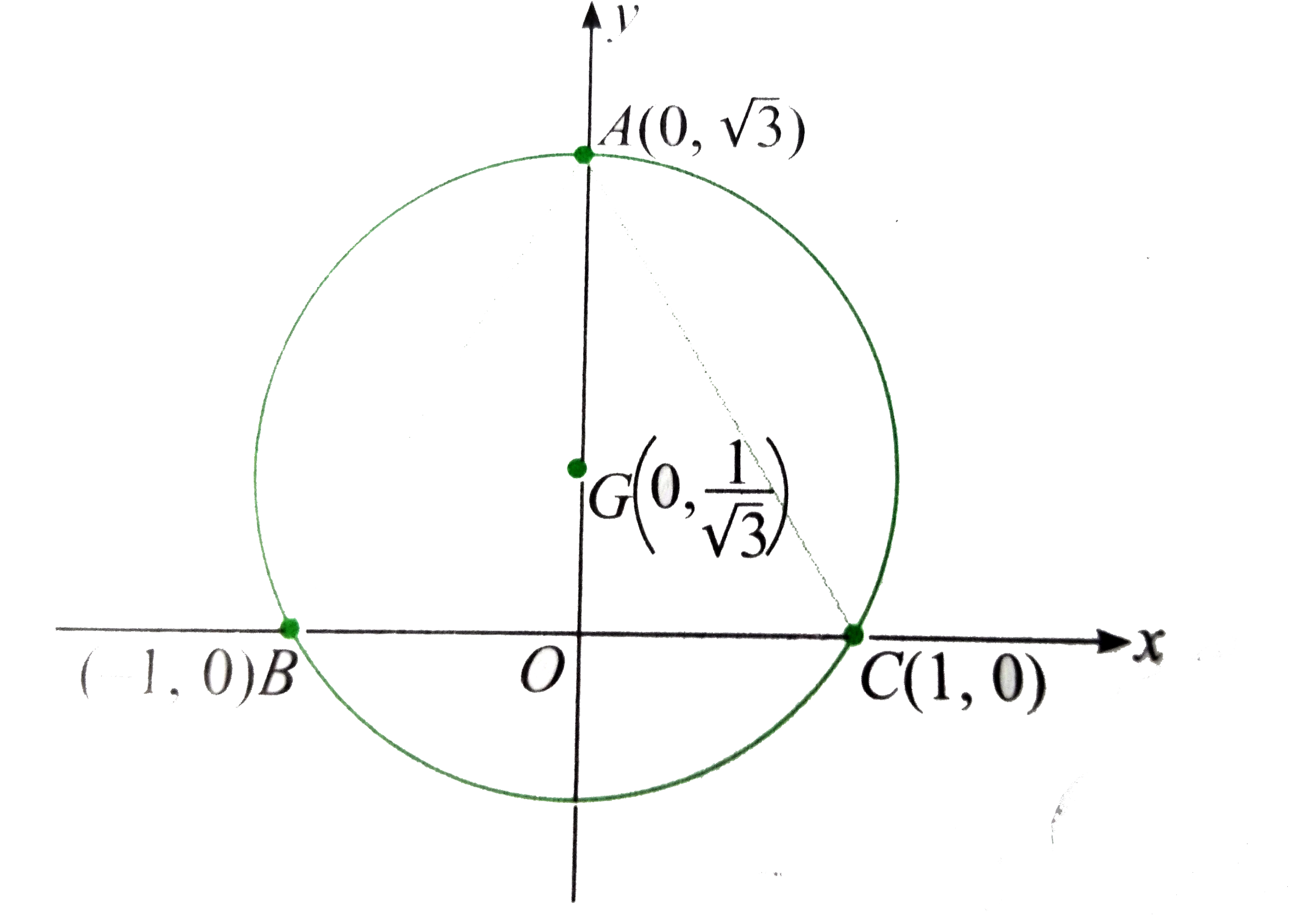
Text Solution
Verified by Experts
|
Topper's Solved these Questions
CIRCLE
CENGAGE|Exercise Exercise 4.1|14 VideosView PlaylistCIRCLE
CENGAGE|Exercise Exercise 4.2|5 VideosView PlaylistBINOMIAL THEOREM
CENGAGE|Exercise Comprehension|11 VideosView PlaylistCIRCLES
CENGAGE|Exercise Question Bank|16 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CENGAGE-CIRCLE -MATRIX MATCH TYPE
- Two vertices of an equilateral triangle are (-1,0) and (1, 0), and its...
05:44
|
Playing Now - Find the derivative of y = ln(cos x^2).
02:25
|
Play - Let x^(2)+y^(2)+2gx+2fy+c=0 be an equation of circle. Match the follow...
06:38
|
Play - Match the following lists.
13:33
|
Play - Find the derivative of y = ln(2x^3 − x)^2
02:51
|
Play - Find the derivative of y = x ln^3 x.
02:28
|
Play - Match the conics in List I with the statements// expressions in List I...
Text Solution
|
Play