A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
WORK, ENERGY AND POWER
PHYSICS WALLAH|Exercise Level - 2|30 VideosView PlaylistWAVES
PHYSICS WALLAH|Exercise NEET PAST 4 YEARS QUESTIONS |15 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
PHYSICS WALLAH-WORK, ENERGY AND POWER-NEET Past 5 Years Questions
- A point mass m is moved in vertical circle of radius r with help of st...
02:20
|
Play - Body A of mass 4m moving with speed u collides with another body B of ...
06:31
|
Play - A mass m is attached to a thin wire and whirled in a vertical circle. ...
04:23
|
Play - A force F=20+10y acts on a particle in y-direction where F is in Newto...
01:37
|
Play - A body initially rest and sliding along a frictionless trick from a he...
07:17
|
Play - A spring of force constant k is cut into lengths of ratio 1 : 2 : 3. T...
04:34
|
Play - Consider a drop of rain water having mass 1 g falling from a height of...
03:20
|
Play - A body initially at rest, breaks up into two pieces of masses 2 M and ...
Text Solution
|
Play - A body is moving unidirectionally under the influence of a source of c...
06:19
|
Play - A particle moves From a point (-2hati+5hatj)" to" (4hatj+3hatk) When a...
01:59
|
Play - Two identical balls A and B having velocity of 0.5 m//s and -0.3 m//s ...
01:47
|
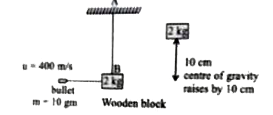
Play - A bullet of mass 10 g moving horizontally with a velocity of 400ms^(-1...
03:18
|
Playing Now - A body of mass 1 kg begins to move under the time dependent force F= 2...
Text Solution
|
Play - A piece of ice falls from a height h so that it melts completely. Only...
02:13
|
Play - What is the minimum velocity with which a body of mass m must enter a ...
04:45
|
Play - A particle of mass 10 g moves along a circle of radius 64 cm with a co...
08:16
|
Play