Home
Class 11
PHYSICS
Figure shows a string of linear mass den...

Figure shows a string of linear mass density `1.0g cm^(-1)` on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of `50 cm` on the string. Take `g = 10 ms^(-2)`

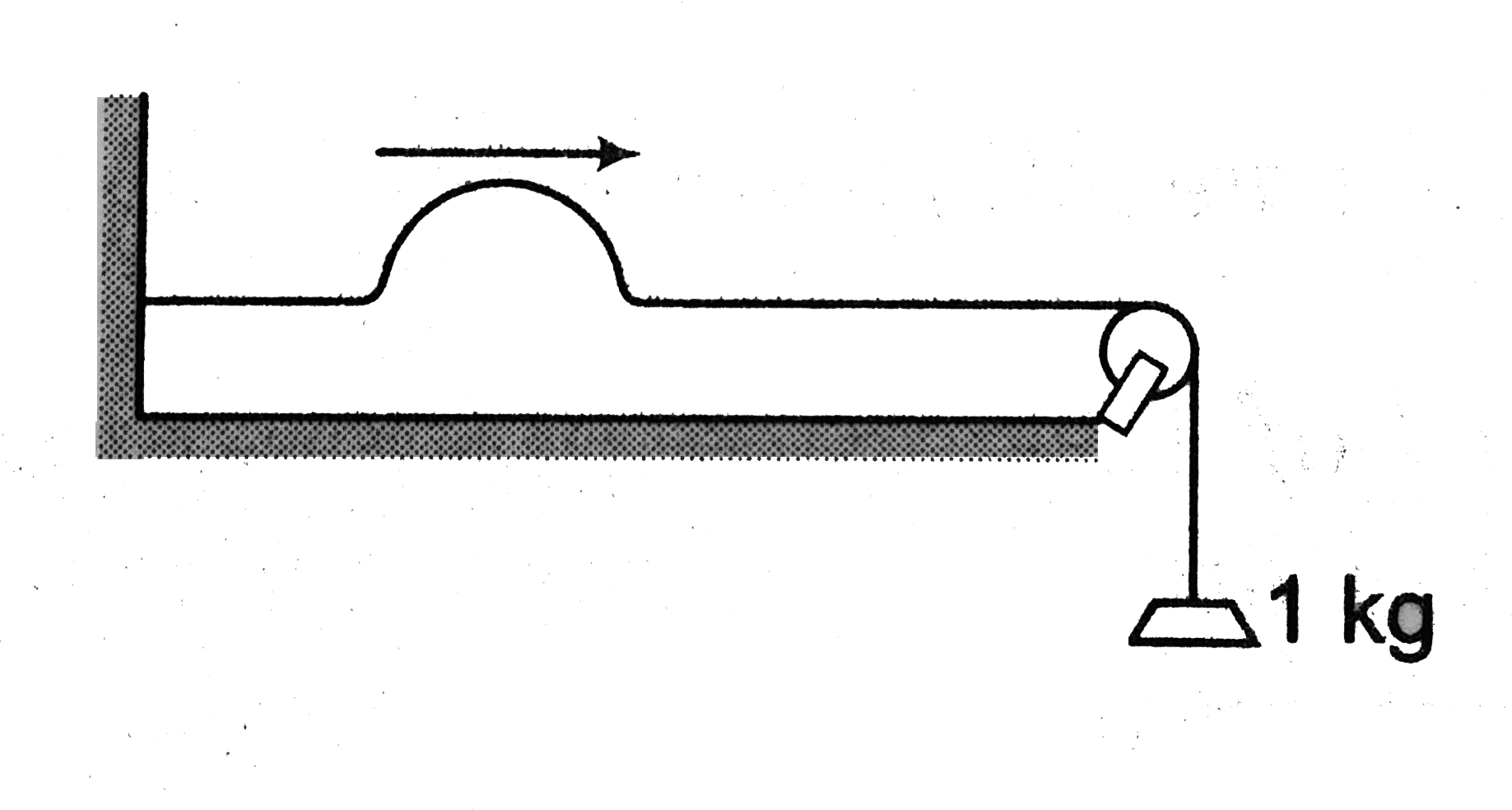
Text Solution

Verified by Experts

The correct Answer is:
`0.05 s`
`v=sqrt((1xx10)/(10^(-3)//10^(-2)))=10m//s,t=(L)/(v)=(0.5)/(10)=0.05 sec`
Promotional Banner

Topper's Solved these Questions

  • WAVES AND OSCILLATIONS

    ALLEN |Exercise Part-1(Exercise-04)[B]|13 Videos

  • WAVES AND OSCILLATIONS

    ALLEN |Exercise Part-1(Exercise-05)[A]|28 Videos

  • WAVES AND OSCILLATIONS

    ALLEN |Exercise Part-1(Exercise-03)|31 Videos

  • SEMICONDUCTORS

    ALLEN |Exercise Part-3(Exercise-4)|50 Videos

Similar Questions

Explore conceptually related problems

A uniform string of length 20m is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the support is : (take g = 10ms^(-2) )

One end of a long string of linear mass density 8.0 xx 10^(-3) kg m^(-1) is connected to an electrically driven tuning fork of frequency 256Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0, the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describes the wave on the string.

A progressive wave on a string having linear mass density rho is represented by y=A sin((2 pi)/(lamda)x-omegat) where y is in mm. Find the total energy (in mu J ) passing through origin from t=0 to t=(pi)/(2 omega) . [Take : rho = 3 xx 10^(-2) kg//m , A = 1mm , omega = 100 rad..sec , lamda = 16 cm ].

In the system shown in figure all surface are smooth, string in massless and inextensible. Find: (a) acceleration of the system (b) tensionin the string and (c ) ectension in the spring if force constant of spring is k = 50 N/m (Take g = 10 m//s^(2) )

What is the acceleration of the block and trolley system show n in a figure, if the coefficient of kinetic friction betw een the trolley and the surface is 0.04 ? What is the tension in the string ? (Take g = 10 ms^(2) ). Neglect the mass of the string.

If velocity (in ms^(-1) ) varies with time as V = 5t, find the distance travelled by the particle in time interval of t = 2s to t = 4 s.

The equation of a wave on a string of linear mass density 0.04 kgm^(-1) is given by y = 0.02(m) sin[2pi((t)/(0.04(s)) -(x)/(0.50(m)))] . Then tension in the string is

What is the acceleration of the block and trolley system shown in if the coefficient of kinetic friction between the trolley and the surface is 0 .04 ? What is the tension in the string ? Take g = 10 ms^(-2) Neglect the mass of the string .

ALLEN -WAVES AND OSCILLATIONS-Part-1(Exercise-04)[A]
  1. A steel wire of length 1 m and mass 0.1 kg and having a uniform cross-...

    Text Solution

    |

  2. In the arrangement shown in figure, the string has a mass of 4.5 g. Ho...

    Text Solution

    |

  3. Figure shows a string of linear mass density 1.0g cm^(-1) on which a w...

    Text Solution

    |

  4. A string vibrate according to the equation y = 5 sin ((pi x)/(3)) cos ...

    Text Solution

    |

  5. A bat emits ultrasonic sound of frequency 100 kHz in air. If this soun...

    Text Solution

    |

  6. The vibrations of a string of length 60cm fixed at both ends are repre...

    Text Solution

    |

  7. Given below are some functions of x and t to represent the displacemen...

    Text Solution

    |

  8. If the bulk modulus of water is 4000 MPa, what is the speed of sound i...

    Text Solution

    |

  9. A steel rod 100 cm long is clamped at its middle. The fundamental freq...

    Text Solution

    |

  10. Two successive resonance frequencies in an open organ pipe are 1944 Hz...

    Text Solution

    |

  11. A flute which we treat as a pipe open at both ends is 60 cm long. (a) ...

    Text Solution

    |

  12. A string 25cm long and having a mass of 2.5 gm is under tension. A pip...

    Text Solution

    |

  13. Two tuning fork having frequency 300 Hz & 305 Hz produce beat phenomen...

    Text Solution

    |

  14. Two sitar strings A and B playing the note 'Dha' are slightly out of ...

    Text Solution

    |

  15. A source of sound of frequency 256 Hz is moving towards a wall with a ...

    Text Solution

    |

  16. A person going away from a factory on his scooter at a speed of 36 km/...

    Text Solution

    |

  17. A car has two horns having a difference in frequency of 180 Hz. The ca...

    Text Solution

    |

  18. A whistle emitting a sound of frequency 440 Hz is tied to string of 1....

    Text Solution

    |

  19. Two tuning forks with natural frequencies of 340 Hz each move relative...

    Text Solution

    |

  20. A SONAR system fixed in a submarine operates at a frequency 40.0kHz. A...

    Text Solution

    |