Home
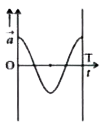
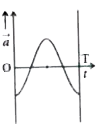
Class 12
PHYSICS
The equation of motion of a particle of ...

The equation of motion of a particle of mass `1g` is `(d^(2)x)/(dt^(2)) + pi^(2)x = 0`, where `x` is displacement (in m) from mean position. The frequency of oscillation is (in Hz)

A

`1/2`

B

`2`

C

`5sqrt(10)`

D

`(1)/(5sqrt(10))`

Text Solution

Verified by Experts

The correct Answer is:
A
`omega^(2) = pi^(2) rArr omega = pi = f = (omega)/(2pi) = (1)/(2)Hz`
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise Exercise-02|19 Videos

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise Exercise- 3 Match The Column|1 Videos

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise SOME WORKED OUT EXAMPLES|29 Videos

  • RACE

    ALLEN |Exercise Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)|25 Videos

  • TEST PAPER

    ALLEN |Exercise PHYSICS|4 Videos

Similar Questions

Explore conceptually related problems

The equation of motion of a particle is x= a cos (alpha t)^(2) . The motion is………..

Acceleration of a particle a= -bx , where x is the displacement of particle from mean position and b is constant. What is the periodic time of oscillation ?

The vertical motion of a ship at sea is described by the equation (d^(x))/(dt^(2))=-4x , where x is the vertical height of the ship (in meter) above its mean position. If it oscillates through a height of 1 m then find the maximum velocity and acceleration

The oscillation of a body on a smooth horizontal surface is represented by the equation x= A cos omega t where x = displacement at time t, omega= frequency of oscillation. Which of the following graphs shows the corrects variation of acceleration 'a' with time 't'.

A simple harmonic motion of a particle is represented by an equation x= 5 sin(4t -(pi)/(6)) , where x is its displacement. If its displacement is 3 unit then find its velocity.

Find dimensional formula: (i) (dx)/(dt) (ii) m(d^(2)x)/(dt^(2)) (iii) int vdt (iv) int adt where x rarr displacement, t rarr time, v rarr velocity and a rarr acceleration

In the equation of motion of waves in x-direction is given by y= 10^(-4) sin(600t-2x+(pi)/(3)) where x and y are in metre and t is in second, then the velocity of wave will be………… ms^(-1) .

A particle of mass m moves in a one dimensional potential energy U(x)=-ax^2+bx^4 , where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to

An object of mass m is attached to a spring. The restroing force of the spring is F - lambdax^(3) , where x is the displacement. The oscillation period depends on the mass, l mabd and oscillation amplitude. Suppose the object is initially at rest. If the initial displacement is D then its period is tau . If the initial displacement is 2D , find the period.

If a simple harmonic motion is represented by (d^(2)x)/(dt^(2))+αx=0 , its time period is.

ALLEN -SIMPLE HARMONIC MOTION-Exercise-01
  1. The equation of motion of a particle of mass 1g is (d^(2)x)/(dt^(2)) +...

    Text Solution

    |

  2. Two bodies performing S.H.M. have same amplitude and frequency. Their ...

    Text Solution

    |

  3. The figure shows the displacement-time graph of a particle executing S...

    Text Solution

    |

  4. Two particles execute SHM of same amplitude and frequency on parallel ...

    Text Solution

    |

  5. A small mass executes linear SHM about O with amplitude a and period T...

    Text Solution

    |

  6. Two particles A to B perform SHM along the same stright line with the ...

    Text Solution

    |

  7. A particle exectes S.H.M. along a straight line with mean position x =...

    Text Solution

    |

  8. A particle performing SHM is found at its equilibrium position at t = ...

    Text Solution

    |

  9. The diagram shows two oscillations. What is the phase difference betwe...

    Text Solution

    |

  10. An object of mass m is attached to a spring. The restroing force of th...

    Text Solution

    |

  11. A particle performs SHM in a straight line. In the first second, start...

    Text Solution

    |

  12. A particle is subjected to two mutually perpendicular simple harmonic ...

    Text Solution

    |

  13. The period of a particle in SHM is 8s. At t=0 it is at the mean positi...

    Text Solution

    |

  14. A particle executes SHM with time period T and amplitude A. The maximu...

    Text Solution

    |

  15. The time taken by a particle performing SHM to pass from point A and B...

    Text Solution

    |

  16. The P.E. of an oscillation particle at rest position is 10J and its av...

    Text Solution

    |

  17. Block A in the figure is released from the rest when the extension in ...

    Text Solution

    |

  18. A system is shown in the figure. The time period for small oscillatio...

    Text Solution

    |

  19. A block of mass 0.9 kg attached to a spring of force constant k is lyi...

    Text Solution

    |

  20. The length of a spring is alpha when a force of 4N is applied on it an...

    Text Solution

    |