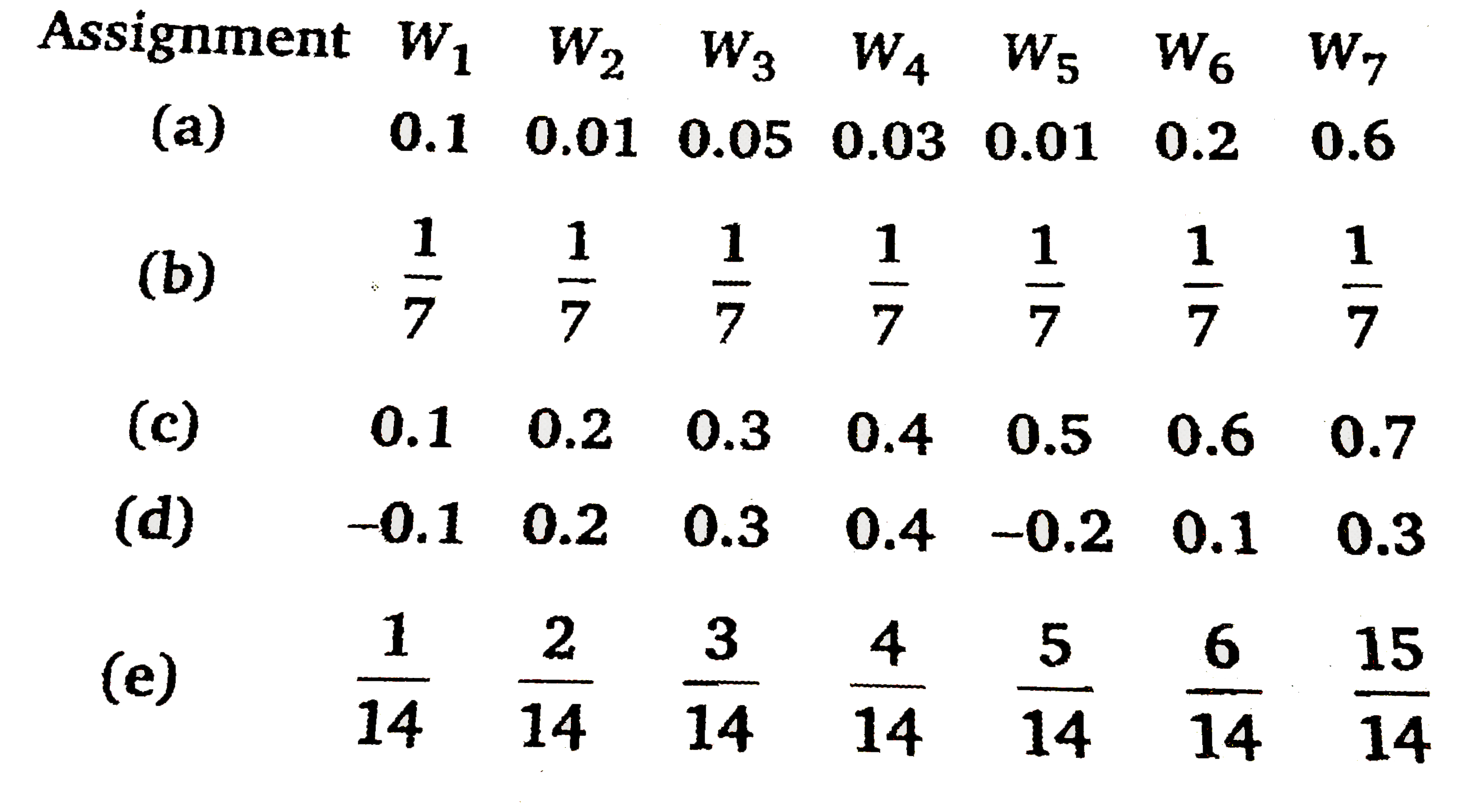Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
PROBABILITY I
CENGAGE PUBLICATION|Exercise Exercise 9.2|19 VideosPROBABILITY I
CENGAGE PUBLICATION|Exercise Exercise 9.3|7 VideosPROBABILITY I
CENGAGE PUBLICATION|Exercise Solved Example|9 VideosPROBABILITY
CENGAGE PUBLICATION|Exercise All Questions|470 VideosPROBABILITY II
CENGAGE PUBLICATION|Exercise MULTIPLE CORRECT ANSWER TYPE|6 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-PROBABILITY I -Exercise 9.1
- Which of the following cannot be valid assignment of probabilities for...
Text Solution
|
- Consider the following assignments of probabilities for outcomes of sa...
Text Solution
|
- Find the probability that a leap year will have 53 Friday or 53 Sat...
Text Solution
|
- A die is loaded so that the probability of a face i is proportional ...
Text Solution
|
- Statement 1: The probability of drawing either an ace or a king from...
Text Solution
|
- Three faces of a fair dice are yellow, two are red and one is blue. Fi...
Text Solution
|