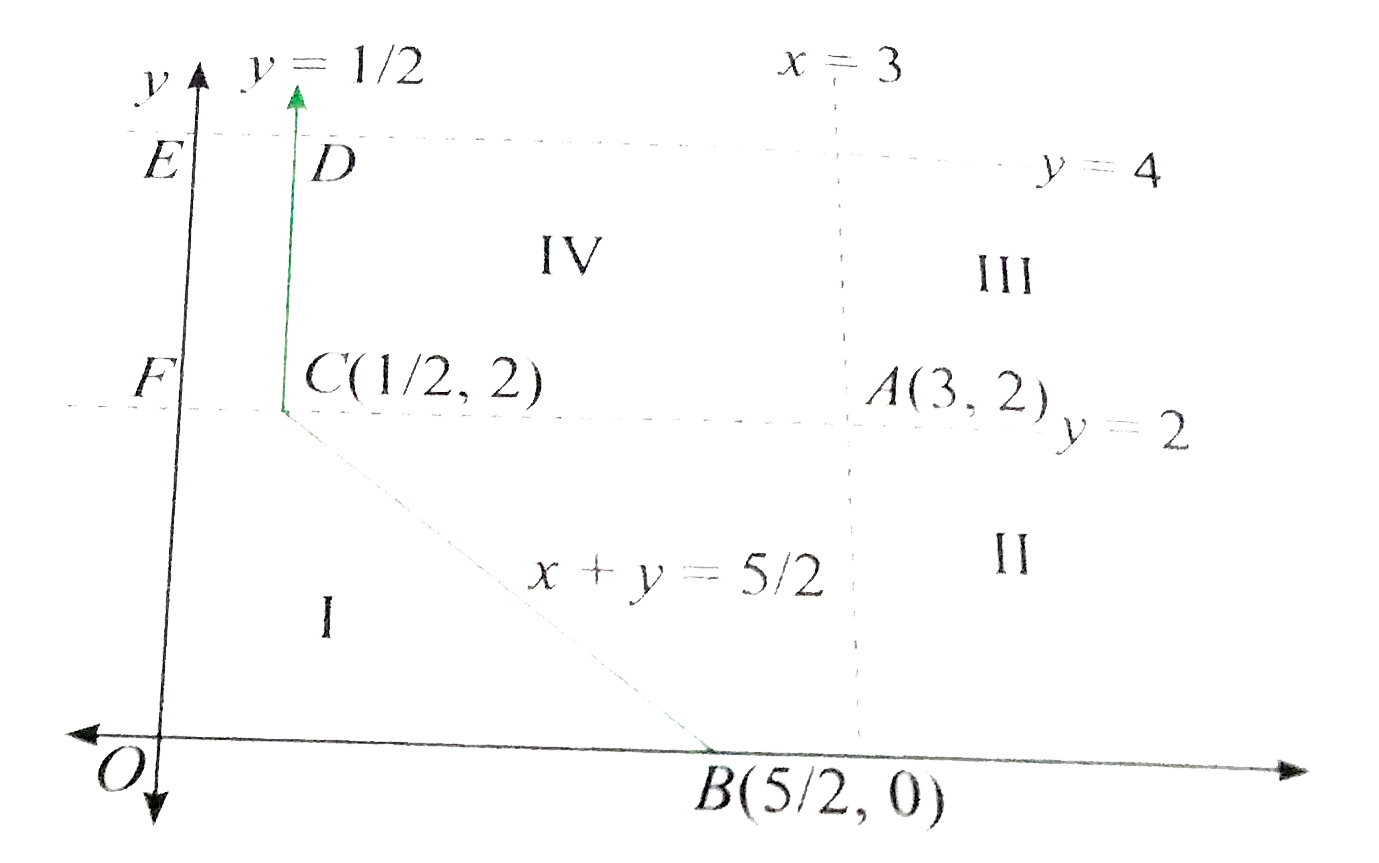
For points P=(x1,y1)and Q =(x2,y2) of th...

For points `P=(x_1,y_1)`and `Q =(x_2,y_2)` of the co-ordinate plane a new distance d(P,Q)=`|x_1-x_2|+|y_1-y_2|` is defined .Let O(0,0)and A(3,2). The set of points in first quadrant which are equidistant from O and A is

one straight line only

union of two line segments

union of two infinite rays

union of a line segment of finite length and an infinite ray

Verified by Experts

The correct Answer is:

Obviously, the locus of P is the union of line segment and one infinite ray.

COORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Matrix match type|4 Videos
COORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Numerical value|12 Videos
COORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Multiple correct|13 Videos
COORDINATE SYSTEM
CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|2 Videos
CROSS PRODUCTS
CENGAGE PUBLICATION|Exercise DPP 2.2|13 Videos

For points P-=(x_1y_1) and Q-=(x_2,y_2) of the coordinate plane, a new distance d(P,Q) is defined by d (P,Q)=|X_1-X_2|+|y_1-y_2| Let O=(0,0),A=(1,2), B-=(2,3) and C-=(4,3) are four fixed points on x-y plane Answer the following questions based on above passage: Let R (x,y), such that R is equidistant from the points O and A with respect to new distance and if 0 < x < 1 and 0 < y < 2 then R lie on a line segment whose equation is

x+y=3

x+2y=3

2x+y=3

2x+2y=3

a line segment of finite length

a line of infinite length

a ray of finite length

a ray of infinite length

6 (x + y) - 25 = 0

2x + 6y + 1= 0

2x + 3y - 6 = 0

6 (x + y) + 25 = 0