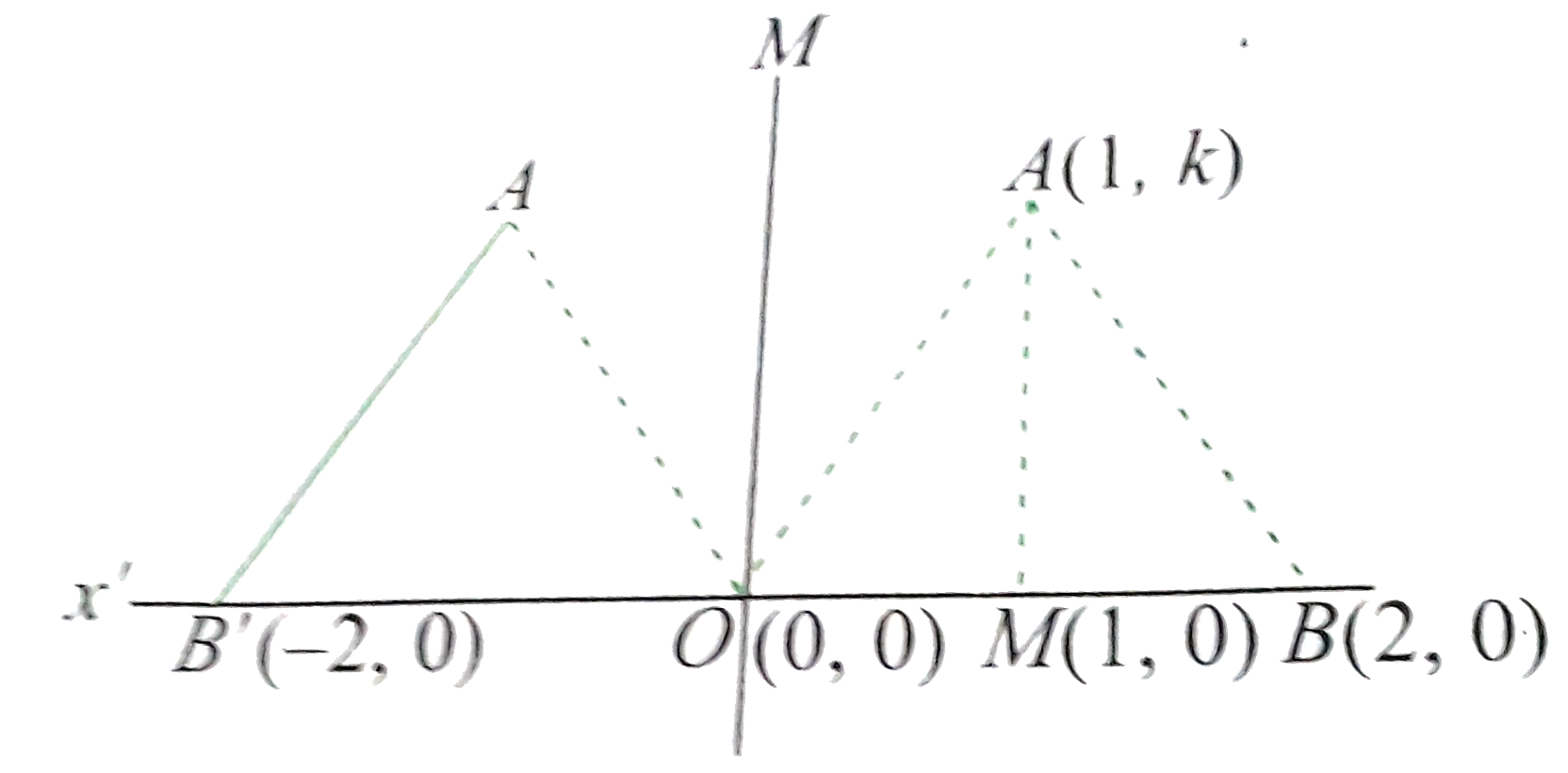
From the figure ,`Delta ABC` is equilateral. Hence,
`tan60^@=k`
i.e., `k=sqrt(3)` (for first quadrant)
or `k=-sqrt(3)` (for fourth quadrant)
then the possible coordinates are `(1,+-sqrt(3))`.
Similarly , for the second quadrant, the point is `(-1,sqrt(3))` and for the third quadrant , the point is `(-1,-sqrt(3))`.
(b) Case i :
If `OA=AB`, then `angleA=30^@`, Therefore
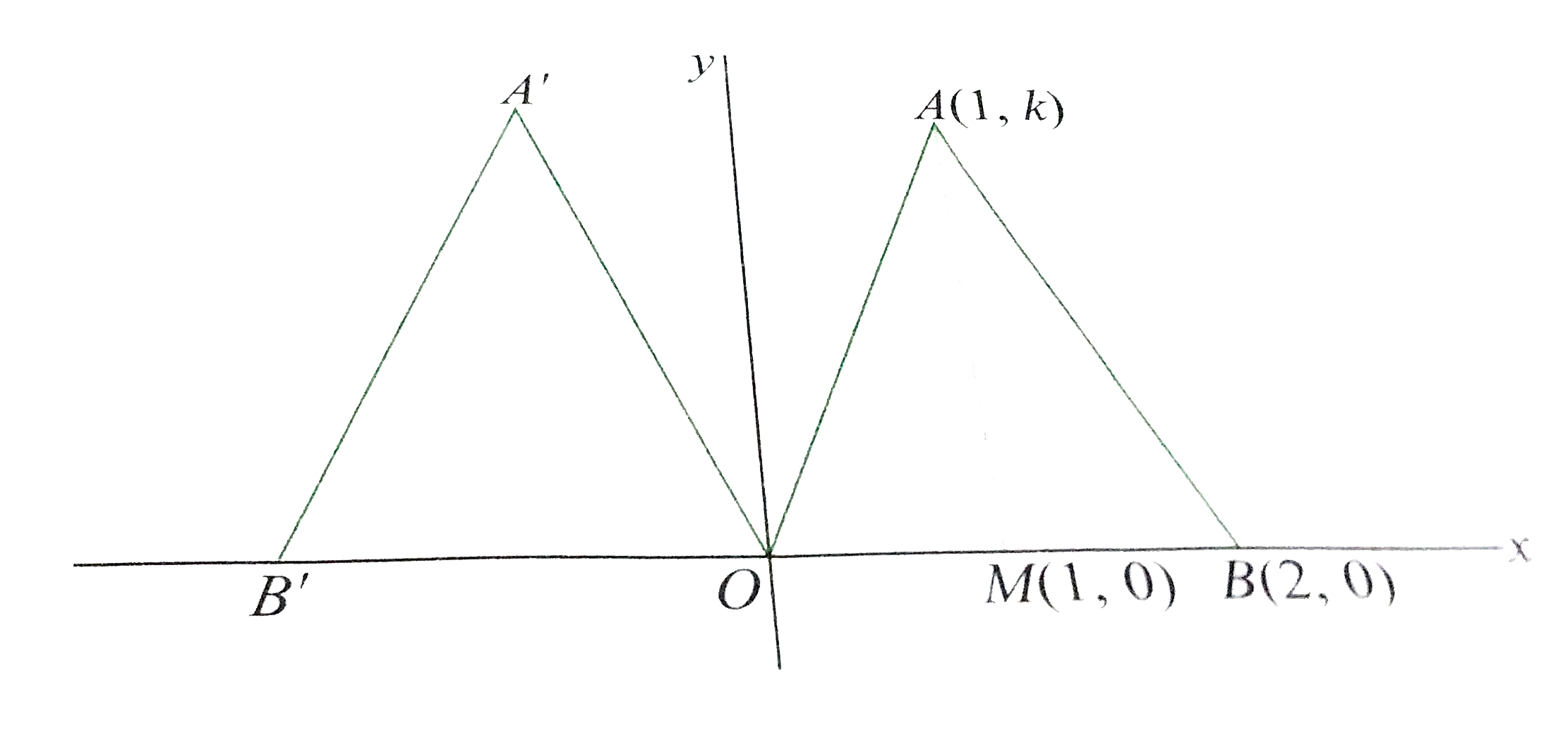
`angle AOB=75^@`
`therefore (AM)/(OM)=tan75^(@`
`AM=OMtan75^@`
`k=1xx(2+sqrt(3))`
`therefore k=2+sqrt(3)`
Hence, point A is `(1,2+sqrt(3))`. By symmetry, all possible points are `(+-1,+-(2+sqrt(3)))`.
Case ii:
`AO=OB`
`therefore angle AOB=120^@`
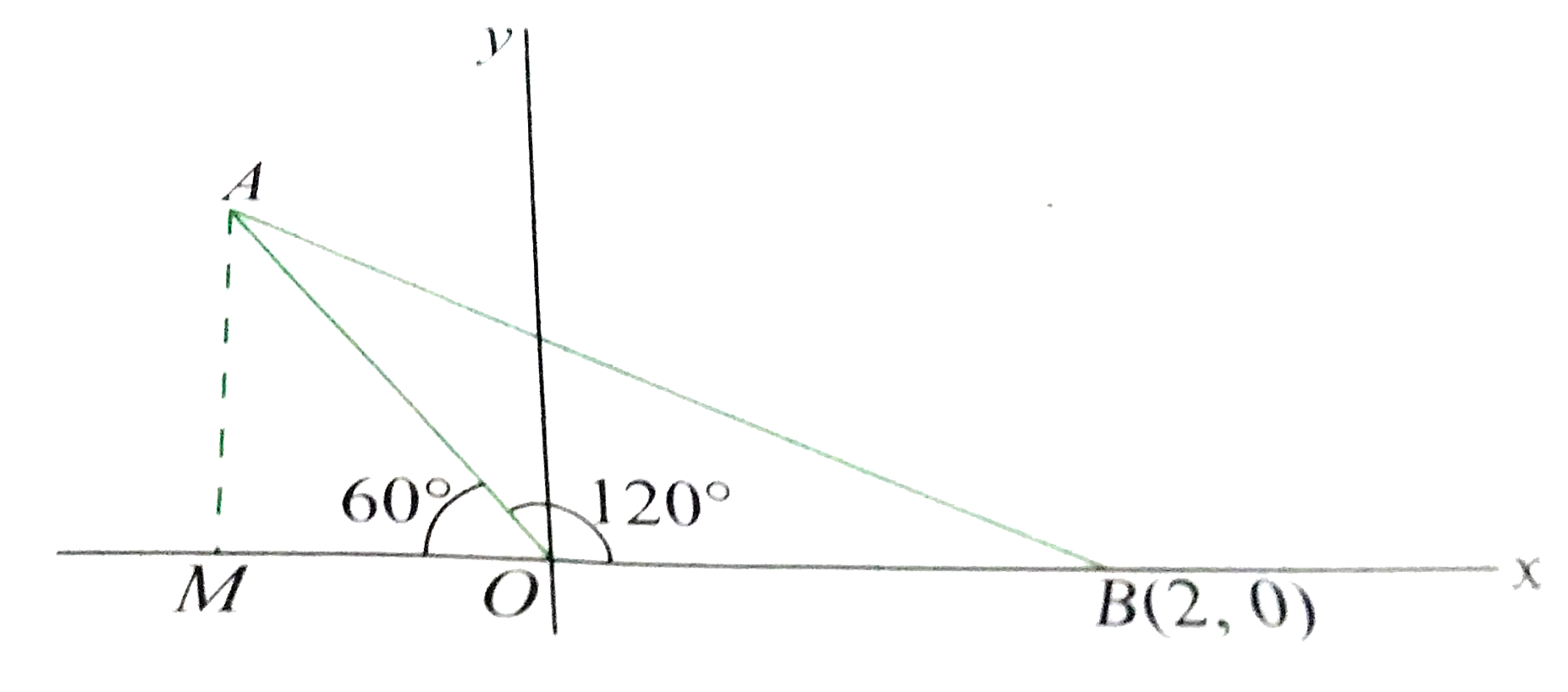
`AM=2 sin 60^@=sqrt(3)`
and `OM=2cos60^@=1`
Hence, point A is `(-1,-sqrt(3))`, By symmetry, all possible points are `(+-1,+-sqrt(3))`.
(c).
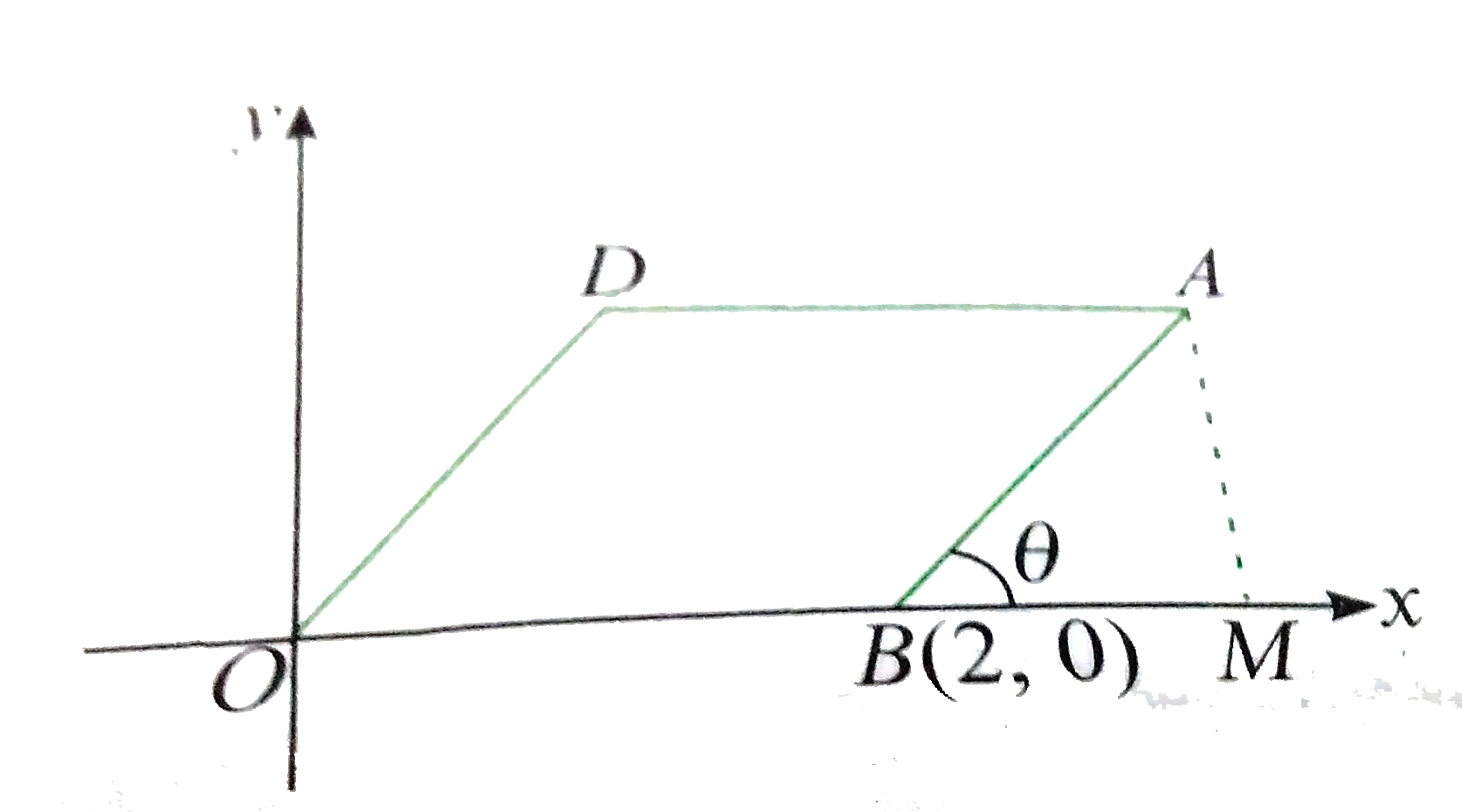
Let `angleDOB =angleABM=theta`.
Area of `DeltaOAB =(1)/(2)xxOBxxAM=(1)/(2)xx2sqrt(3)`
or `2xx2sintheta=2sqrt(3)`
or `sintheta=(sqrt(3))/(2)`
or `AM=sqrt(3) and BM=1`
Hence, A has coordinates `(3,sqrt(3))`, By symmetry, all the possible coordinates are `(+-3,+-sqrt(3))`.
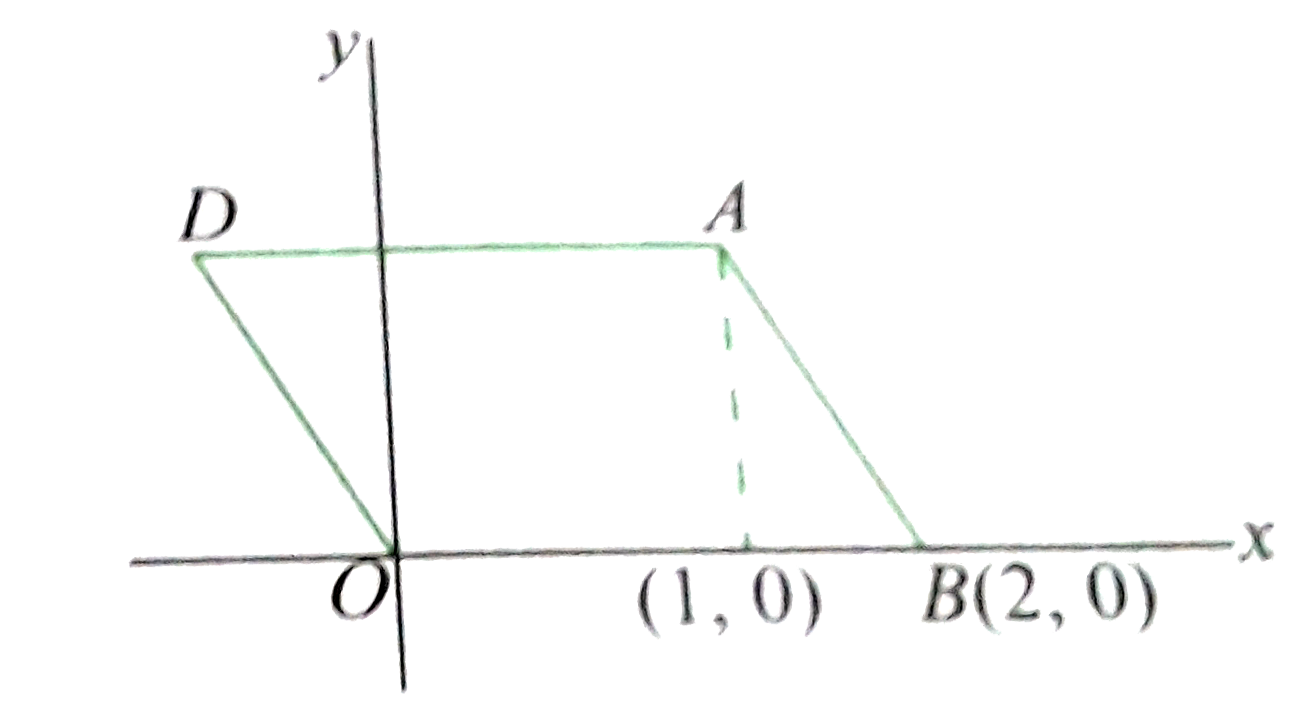
From the figure, A has coordinates `(1,sqrt(3))`.
By symmetry, all possible coordinates are `(+-,+-sqrt(3))`.
(d)

`OB=2units =OO'= "Radius"`
or `OM=(2)/(2)=1"unit"`
In `DeltaOO'M`,
`O'M=sqrt(4-1)=sqrt(3)`
Since `DeltaOAB` is isosceles, point A lies on the perpendicular bisector of OB. Therefore,
`AM=sqrt(3)+2=OM+OA`
Hence, the coordinates of A will be `(1,2+sqrt(3))` in the first quadrant. By symmetry, all possible coordinates of A are `(+-1,+-(2+sqrt(3))`.






