A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CIRCLES
CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|9 VideosView PlaylistCIRCLE
CENGAGE PUBLICATION|Exercise For problems 3 and 4|2 VideosView PlaylistCOMPLEX NUMBERS
CENGAGE PUBLICATION|Exercise MULTIPLE CORRECT ANSWER TYPE|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-CIRCLES-Comprehension Type
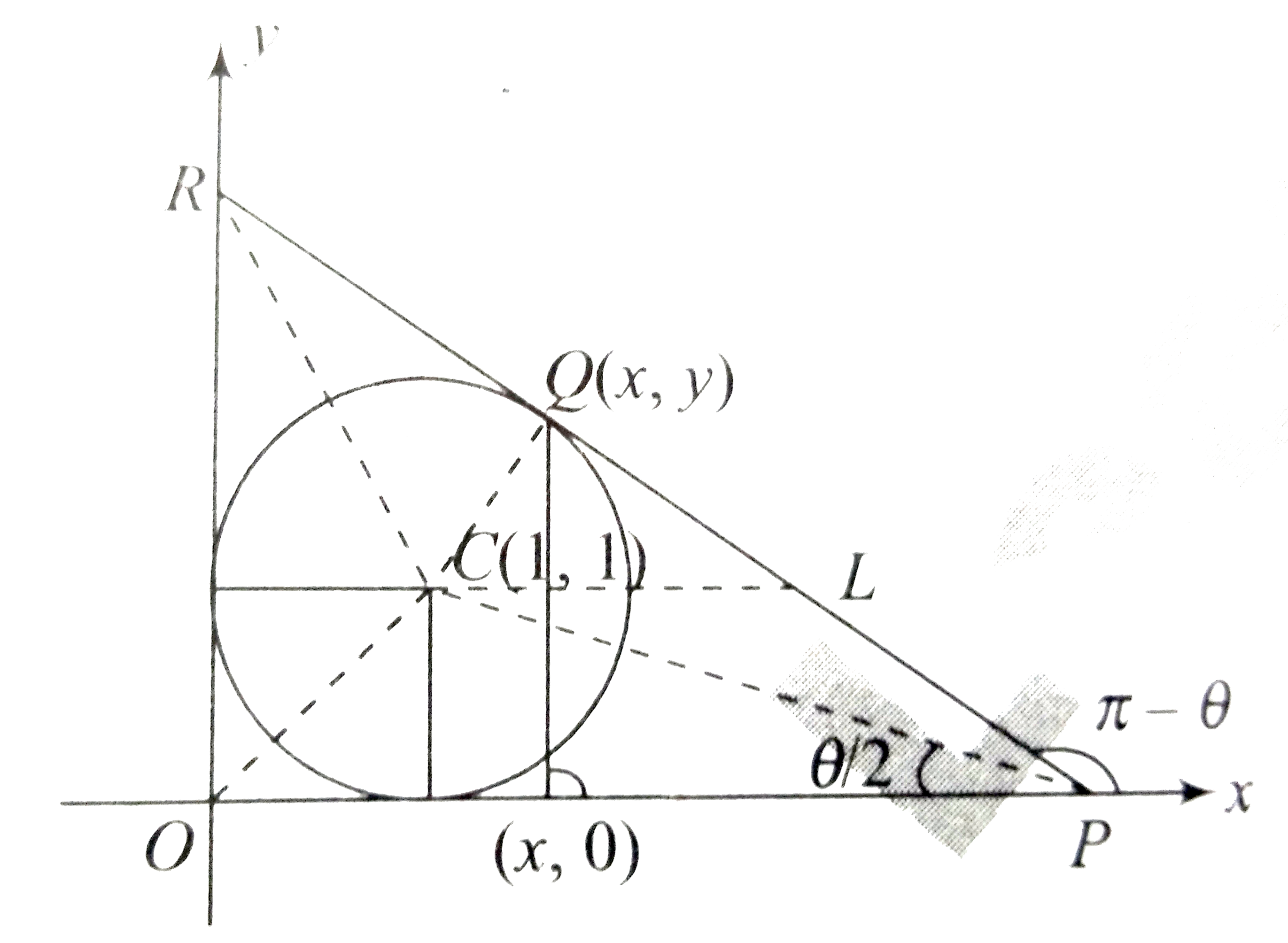
- In the diagram as shown, a circle is drawn with centre C(1,1) and radi...
02:14
|
Playing Now - In the diagram as shown, a circle is drawn with centre C(1,1) and radi...
Text Solution
|
Play - In the diagram as shown, a circle is drawn with centre C(1,1) and radi...
Text Solution
|
Play - Let P(alpha,beta) be a point in the first quadrant. Circles are drawn ...
06:08
|
Play - P(α,β) is a point in first quadrant. If two circles which passes throu...
07:02
|
Play - Let P(alpha,beta) be a point in the first quadrant. Circles are drawn ...
05:04
|
Play - P(a,5a) and Q(4a,a) are two points. Two circles are drawn through thes...
03:10
|
Play - Two circles are drawn through the points (a,5a) and (4a, a) to touch t...
07:16
|
Play