Home
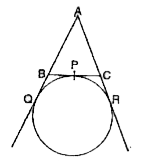
Class 8
MATHS
In the figure shown here, a circle touch...

In the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?

A

One-third of the perimeter of `Delta` ABC.

B

Half of the perimeter of `Delta` ABC.

C

Two-third of the perimeter of `Delta` ABC

D

Three-fourth of the perimeter of `Delta` ABC

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    S CHAND IIT JEE FOUNDATION|Exercise QUESTION BANK - 39|1 Videos

  • CIRCLES

    S CHAND IIT JEE FOUNDATION|Exercise QUESTION BANK - 40|1 Videos

  • CIRCLES

    S CHAND IIT JEE FOUNDATION|Exercise QUESTION BANK - 37|1 Videos

  • AVERAGE

    S CHAND IIT JEE FOUNDATION|Exercise SELF ASSESSMENT SHEET|10 Videos

  • CO-ORDINATE GEOMETRY

    S CHAND IIT JEE FOUNDATION|Exercise Self Assessment Sheet |10 Videos

Similar Questions

Explore conceptually related problems

A circle touches the side BC of DeltaABC at P and touches AB and AC produced at Q and R respectively. Prove that AQ=1/2(Perimeter of DeltaABC).

A circle is touching the side BC of ABC at P and touching AB and AC produced at Q and R respectively.Prove that AQ=(1)/(2)(Perimeter of ABC)

A circle touches the side BC of a Delta ABC at P and also touches AB and AC produced at Q and R, respectively. If the perimeter of Delta ABC = 26.4 cm, then the length of AQ is:

A circle touches the side BC of DeltaABC at D and AB and aC are produced to E and F, respectively. If AB=10cm, AC=8.6 cm and BC=6.4 cm then BE=?

A circle is touching the side BC of Delta ABC at P and touching AB and AC produced at Q and R respectively Prove that AQ=(1)/(2) (Perimeter of Delta ABC)

A circle touches the side BC of Delta ABC at F and touches AB and AC at D and E, respectively. If AD = 8 cm, then find the perimeter of Delta ABC .

The sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P Q,and R respectively.

In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.