Home
Class 12
MATHS
To evaluate lim(xtoa)[f(x)], we must ana...

To evaluate `lim_(xtoa)[f(x)]`, we must analyse the `f(x)` in right hand neighbourhood as well as in left hand neighbourhood of `x=a`. E.g. In case of continuous function, we may come across followign cases.


`If `f(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If `f(a)` is not an integer, the limit exists in all the cases. ltbgt If `f'(1)=-3` and `lim_(xto1)[f(x)-1/2]` does not exist, (where [.] denotes the greatest integer function), then

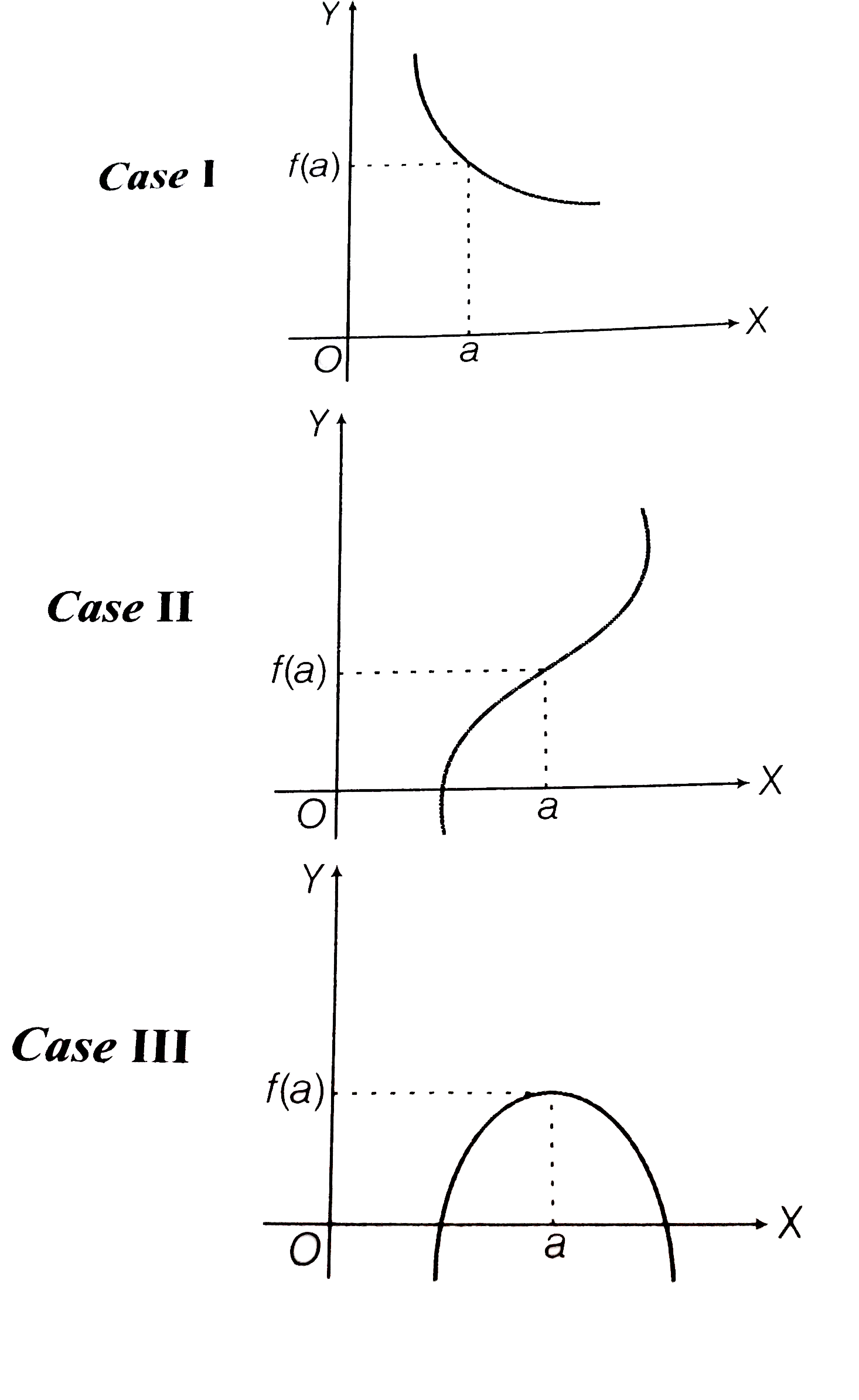
Text Solution

Verified by Experts

The correct Answer is:
A
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • LIMITS

    ARIHANT MATHS|Exercise Exercise (Single Option Correct Type Questions)|38 Videos

  • LIMITS

    ARIHANT MATHS|Exercise Exercise (More Than One Correct Option Type Questions)|15 Videos

  • LIMITS

    ARIHANT MATHS|Exercise Exercise For Session 6|5 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|8 Videos

  • LOGARITHM AND THEIR PROPERTIES

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|4 Videos

Similar Questions

Explore conceptually related problems

To evaluate lim_(xtoa)[f(x)] , we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a . E.g. In case of continuous function, we may come across followign cases. If f(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. lim_(xto1)["cosec"(pix)/2]^(-1//(1-x)) is equal to (where [.] denotes the greatest integer function).

lim_(xtoc)f(x) does not exist when where [.] and {.} denotes greatest integer and fractional part of x

Knowledge Check

  • In case of oxidation, there is

    A
    increase in O.N.
    B
    decrease in O.N.
    C
    no change in O.N.
    D
    none of these

    • Similar Questions

    Explore conceptually related problems

    If f(x)=e^(sin(x-[x])cospix) , where [x] denotes the greatest integer function, then f(x) is

    The function f(x) = [x], where [x] denotes the greatest integer function, is continuous at

    f(x)=log(x-[x]) , where [*] denotes the greatest integer function. find the domain of f(x).

    If the domain of y=f(x) is [-3,2] , then find the domain of g(x)=f([x]), where [] denotes the greatest integer function.

    If f^2(x)*f((1-x)/(1+x))=x^3, [x!=-1,1 and f(x)!=0], then find |[f(-2)]| (where [] is the greatest integer function).

    If f(x) = {{:([x]+[-x]",",x ne 2),(" "lambda",",x = 2):} and f is continuous at x = 2, where [*] denotes greatest integer function, then lambda is

    If f(x)=cos[pi/x] cos(pi/2(x-1)) ; where [x] is the greatest integer function of x ,then f(x) is continuous at :

    Home
    Profile