Text Solution
Verified by Experts
|
Topper's Solved these Questions
GAUSS'S THEOREM
BETTER CHOICE PUBLICATION|Exercise LONG ANSWER TYPE QUESTIONS|9 VideosView PlaylistGAUSS'S THEOREM
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED NUMERICALS|4 VideosView PlaylistGAUSS'S THEOREM
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS |10 VideosView PlaylistFORCE ON A CURRENT
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS|10 VideosView PlaylistHUYGENS' PRINCIPLE
BETTER CHOICE PUBLICATION|Exercise LONG ANSWER TYPE QUESTIONS |11 VideosView Playlist
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-GAUSS'S THEOREM-SHORT ANSWER TYPE QUESTIONS
- What is the use of Gaussian surface in electrostatics ?
03:00
|
Play - What is the importance of Gauss’theorem in electrostatics ?
02:09
|
Play - State and prove Gauss's theorem in electrostatics.
04:26
|
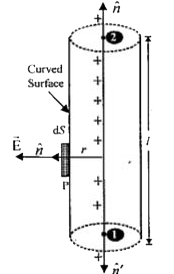
Play - Using Gauss’s law, determine the electric field intensity due to a lon...
02:34
|
Playing Now - State Gauss' law in electrostatics. Using this law, derive an expressi...
04:46
|
Play - State Gauss' theorem in electrostatics. Derive an expression for the e...
05:02
|
Play - State Gauss’s theorem.How Coulomb’s law can be derived from it ?
03:07
|
Play - What is electriG flux ? Explain how the electric flux through a surfac...
06:41
|
Play