Text Solution
Verified by Experts
Topper's Solved these Questions
FORCE ON A CHARGE
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS |14 VideosFORCE ON A CHARGE
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWER TYPE QUESTIONS (MOST EXPECTED QUESTIONS) |3 VideosELECTROSTATIC POTENTIAL
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS (MOST EXPECTED QUESTIONS)|6 VideosFORCE ON A CURRENT
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS|10 Videos
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-FORCE ON A CHARGE -LONG ANSWER TYPE QUESTIONS
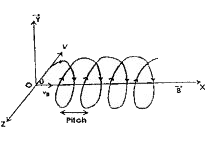
- Discuss the motion of charged particle in uniform magnetic field, when...
Text Solution
|
- What is cycotron? With the help of a labelled diagram explain constru...
Text Solution
|
- What is cycotron? With the help of a labelled diagram explain constru...
Text Solution
|
- Explain the principle, construction and working of a cyclotron with th...
Text Solution
|
- (a) An electric charge in electric field at right angle to the directi...
Text Solution
|