A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
NTA TPC JEE MAIN TEST 55
NTA MOCK TESTS|Exercise PHYSICS (SUBJECTIVE NUMERICAL)|10 VideosView PlaylistNTA TPC JEE MAIN TEST 57
NTA MOCK TESTS|Exercise PHYSICS |30 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
NTA MOCK TESTS-NTA TPC JEE MAIN TEST 56-PHYSICS
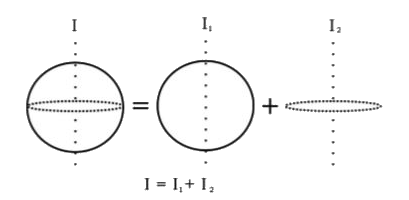
- For zero Magnetic Field at the centre the value of i1/i2 is:
Text Solution
|
Play - A liquid is flowing in a horizontal uniform capillary tube under a con...
02:31
|
Play - If light travels a distance x in t(1) sec in air and 10x distance in t...
02:57
|
Play - Two lenses of flint glass are of focal length 8 cm and 4 cm. What must...
Text Solution
|
Play - Two rings of same radius and mass are placed such that their centres a...
01:31
|
Playing Now - A child is standing with folded hands at the center of a platform rota...
01:51
|
Play - The temperature of an ideal gas undergoing adiabatic expansion varies ...
02:53
|
Play - The maximum intensity of fringes in Young's experiment is I. If one of...
03:10
|
Play - velocity of a body of mass 2kg moving in x-y plane is given by vecv=(2...
01:36
|
Play - Two men with weights in the ratio 4:3 run up a staircase in time in th...
02:39
|
Play - The initial kinetic energy and wavelength for a free electron are E an...
02:35
|
Play - What is the output power (in mW) when input signal is 1.01 mW for the ...
Text Solution
|
Play - As the day advances, the temperature of an open room of volume 41. 6m^...
Text Solution
|
Play - A coil having magnetic moment 15 A m^2 placed in a uniform magnetic f...
Text Solution
|
Play - Four monochromatic and coherent sources of light emitting waves in pha...
12:33
|
Play - Consider a horizontal spring-block system executing SHM. The block has...
Text Solution
|
Play - What is the percentage error in the physical quantity A If it is rela...
02:48
|
Play - Consider two identical cylindrical vessels separated by a valve with t...
Text Solution
|
Play - 6 gm of steam at 100^@ C is mixed with 6 gm of ice at 0^@ C. Find the ...
02:41
|
Play - The radii of two spheres of same material having density p are in the ...
Text Solution
|
Play