Home
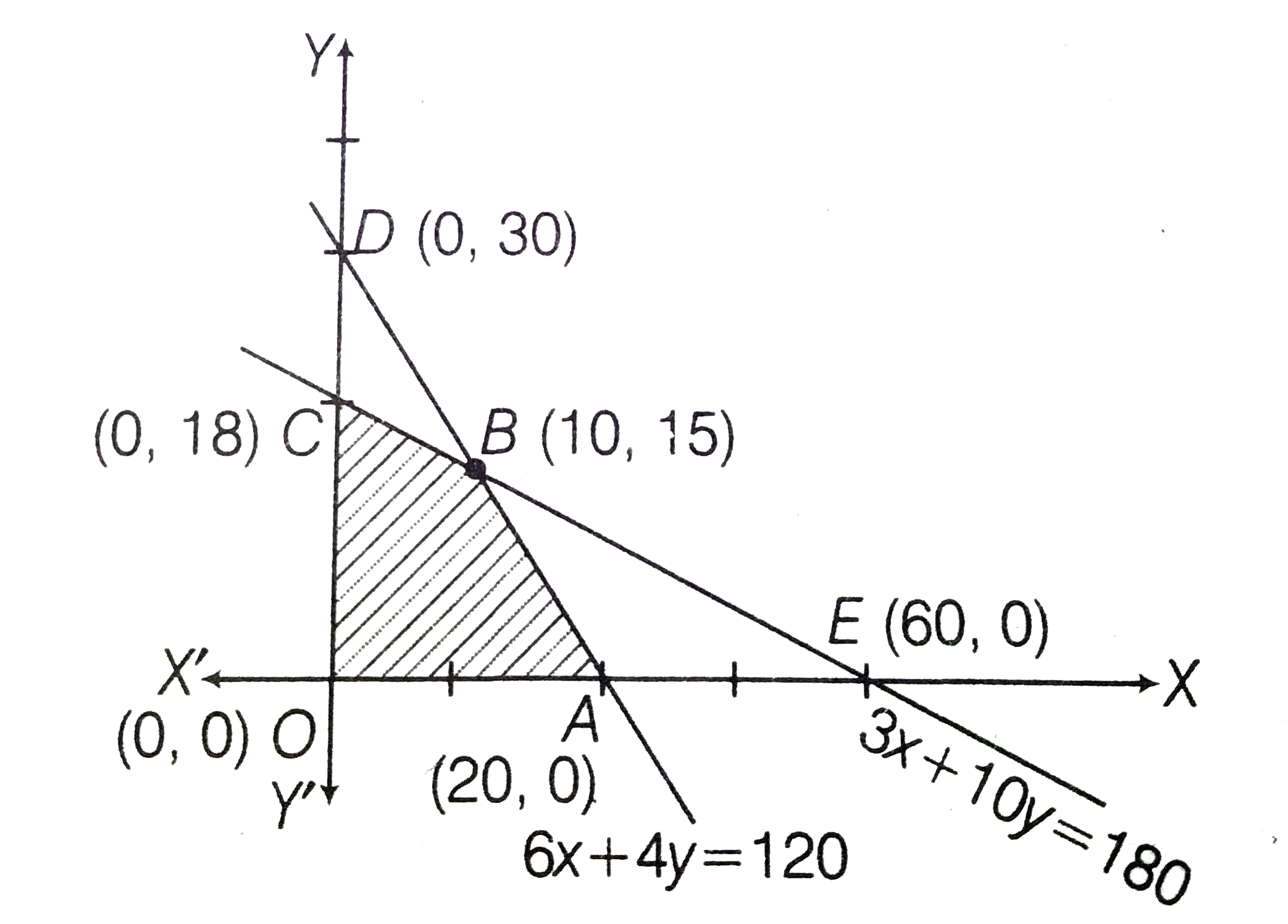
Class 12
MATHS
The point which provides the solution of...

The point which provides the solution of the linear programming problem, maximise Z = 45x + 55y. Subject to constraints Subject to constraints ` x,y ge 0, 6x +4y le 120` and ` 3x +10 y le 180 ` is

A

(15, 10)

B

(10, 15)

C

(0,18)

D

(20,0)

Text Solution

Verified by Experts

The correct Answer is:
B
Given ,constriants are
` 6x+4y le 120`
`3x +10y le 180 `
`x,y ge 10`
Objective function Z=45x+55y is to be maximised .

Here , OABCO is the requred feasible region whose corner points are O, A,B and C ,

Hence, the maximum value of Z is 1275 at B (10,15)
Promotional Banner

Topper's Solved these Questions

  • Linear Programming

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|13 Videos

  • Linear Programming

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )|15 Videos

  • LINE

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|3 Videos

  • MATHEMATICAL LOGIC

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET CORNER|22 Videos

Similar Questions

Explore conceptually related problems

Solve the linear programming problem. Maximise Z = x + 2y Subject to constraints x - y le 10, 2x +3y le 20 and x ge 0, y ge 0

The point which provides the solution of the solution to the linear programming problem . Maximum (2x+3y) subject to constraints . 4x +y ge 4, x +3yge 6,x +y ge 3,x ge 0,y ge 0 is

Consider the linear programming problem Maximise Z = 4x + y. Subject to constraints x+y le 50, x +y ge 100 and x ,y ge 0 Then, maximum vlaue of Z is

The linear programming problem minimiseZ=3x+2y subject to the constraints x+y ge 8 3x +5y le 15 x ge 0, y ge 0 has

Find the corner points of the feasible region of the linear programming problem;,Max Z=x : Subject to the constraints 3x+2y =0,y>=0

By graphical method, the solutions of linear programming problem maximum Z = 3x_1 + 5x_2 subject to constraints 3x_1+2x_2 le 18 x_1 le 4, x_2 le 6,x_1 ge 0, x_2 ge 0

Maximize Z = 400x + 500y subject to constraints x + 2y le 80 ,2x + y le 90, x ge 0 , y ge 0

Solve the Following Linear Programming Problem graphically: Maximise Z=3x+4y subject to the constraints : x+y =0,y>=0

Maximize Z = 5x + 3y subject to the constraints: 3x + 5y le 15, 5x + 2y le 10, x ge 0, y ge 0

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-Linear Programming -EXERCISE 2 (MISCELLANEOUS PROBLEMS )
  1. The point which provides the solution of the linear programming proble...

    Text Solution

    |

  2. Determine the system of linear equation for which the solution set is ...

    Text Solution

    |

  3. if x+y le 2,x ge 0 then point at which maximum value of 3x + 2y at...

    Text Solution

    |

  4. The solution set of the linear inequalities 2x + 2y ge 10 and x+ 2y ...

    Text Solution

    |

  5. Solve the linear programming problem. Maximise Z = x + 2y Subject ...

    Text Solution

    |

  6. For an LPP, minimise Z = 2x + y subject to constraint 5x+10y le 50 , x...

    Text Solution

    |

  7. Consider the inequalities x1+x2 le 3,2x1+5x2ge 10x1,x2 ge 0 then feas...

    Text Solution

    |

  8. Z=4x+2y,4x+2y ge 46, x +3y le 24 and x and y are greater than or equ...

    Text Solution

    |

  9. The minimum vlaue Z = 2x1 +3x2 subject to the conditions 2x1+7x2ge22...

    Text Solution

    |

  10. The maximum value P = 3x + 4y subjected to the constraints x + y le 40...

    Text Solution

    |

  11. Consider the inequalities 5x1+4x2ge9,x1+x2 le 3, x1 ge 0 , x2 ge 0 Wh...

    Text Solution

    |

  12. The minimum and maximum values problem, of Z for the minimise and ma...

    Text Solution

    |

  13. The linear programming problem minimiseZ=3x+2y subject to the constrai...

    Text Solution

    |

  14. The maximum and minimum values of the objective function Z = x + 2y s...

    Text Solution

    |

  15. The maximum value of the objective function Z=3x+4y subject to th...

    Text Solution

    |

  16. Let x and y are the number of tables and chairs respectively, on which...

    Text Solution

    |

  17. The graphical solution of linear inequalities x+y ge 5 " and " x -y ...

    Text Solution

    |

  18. By graphical method, the solutions of linear programming problem maxim...

    Text Solution

    |

  19. A toy company manufactures two types of doll; a basic version doll; a ...

    Text Solution

    |

  20. The minimum value of Z = 10x + By subject to 4x +y ge 4, x +3y ge 6, ...

    Text Solution

    |