Principle : A current-carrying coil suspended in a magnetic field experiences a torque which rotates the plane of the coil to maximize the magnetic flux through the coil.
Proof: Consider a rectangular coil PQRS, of length I, breadth b and carrying a current I suspended in a uniform magnetic field of induction `vecB`. Suppose its plane is parallel to `vecB` as shown in the figure.
The sides QR and sp are parallel to `vecB` so that no force acts on them.
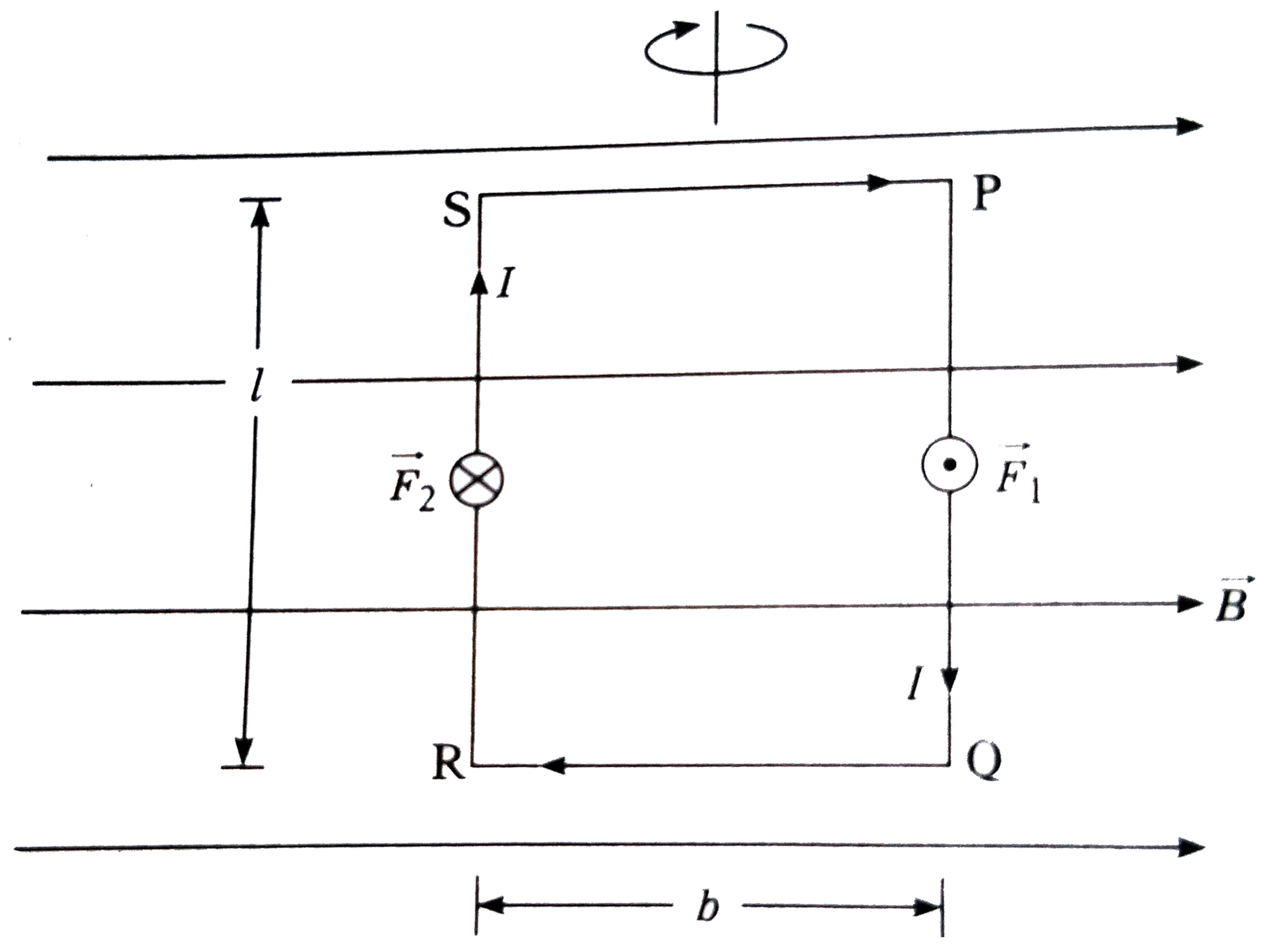
The forces `vecF_(1)` and `vecF_(2)` on the sides PQ and RS are equal in magnitude =IlB, and opposite in direction, but have different lines of action.
According to Fleming's left-hand rule, `vecF_(1)`, is out of the page and `vecF_(2)` is into.
They form a couple and the moment arm of the couple is b (the perpendicular distance between the lines of action of F, and F The magnitude of the deflecting torque due to this couple is
`gamma_d="force" xx "moment arm"= (IlB) b=IAB` ltbr where A= Ib = area of the coil. For a coil of N turns, `gamma_(d)`=NIAB
This torque rotates the coil.
In a moving-coil galvanometer, the coil swings in a radial magnetic field produced by the combination of the cylindrically concave pole pieces and the soft-iron core. In the radial field, the plane of the coil is always parallel to the field lines. Therefore, the deflecting torque is constant and maximum as given by Eq. (1).
The rotation of the coil twists the suspension fibre which exerts a restoring torque on the coil. The restoring torque is Ce, where 0 is the ang of twist and C is the torque constant (torque per unit angle of twist). The coil eventually comes to rest in the position where the restoring torque equal the deflecting torque in magnitude. Therefore, in the equilibrium position.
`therefore C theta=NIAB` ......(3)
`therefore I=((C)/(NAB)) theta` ......(4)
`therefore I alpha theta`
since, N,A,B and C are constant. Thus, the current through the coil is directly proportional to the deflection of the coil.
