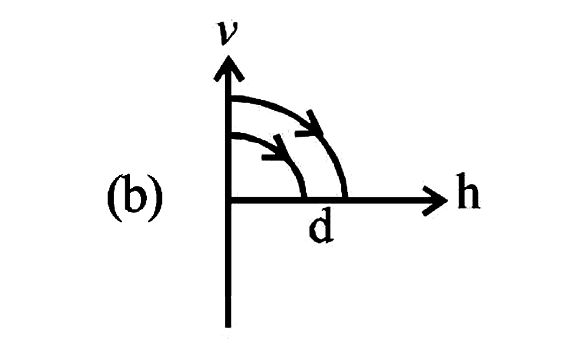
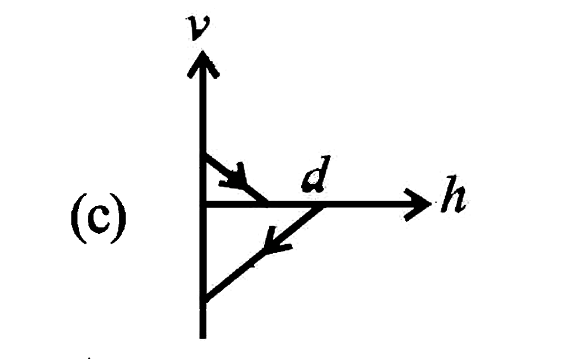
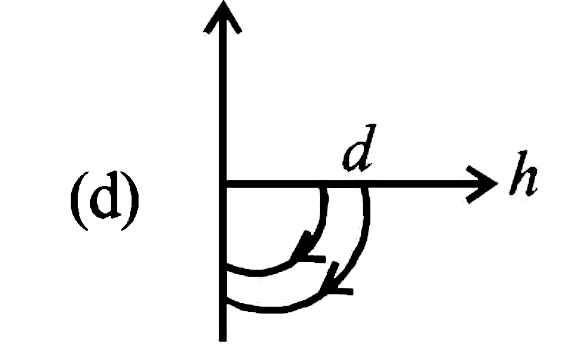
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SUNIL BATRA (41 YEARS IITJEE PHYSICS)-MOTION-JEE Main And Advanced
- A boat which has a speed of 5 km per hour in still water crosses a riv...
Text Solution
|
- In 1.0 s, a particle goes from point A to point B , moving in a semici...
Text Solution
|
- A ball is dropped vertically from a height d above the ground . It hit...
Text Solution
|
- A particle starts sliding down a frictionless inclined plane. If S(n...
Text Solution
|
- A body starts from rest at time t = 0 , the acceleration time graph ...
Text Solution
|
- The velocity - displacement graph of a particle moving along a straigh...
Text Solution
|
- Two identical discs of same radius R are rotating about their axes in ...
Text Solution
|
- Consider a disc rotating in the horizontal plane with a constant angul...
Text Solution
|
- A particle is moving eastwards with a velocity of 5 m//s. In 10 s the...
Text Solution
|
- A particle of mass m moves on the x- axis as follows : it starts fro...
Text Solution
|
- The coordinate of a particle moving in a plane are given by x(t) = ...
Text Solution
|
- A car accelerates from rest at a constant rate alpha for some time, af...
Text Solution
|
- The displacement x of particle moving in one dimension, under the acti...
Text Solution
|
- Answer the following giving reasons in brief : Is the time variati...
Text Solution
|
- Particles P and Q of mass 20g and 40g respectively are simu ltaneously...
Text Solution
|
- Two towers AB and CD are situated at a distance d apart, as shown in ...
Text Solution
|
- Two guns situated at the top of a hill of height 10 m fire one shot ea...
Text Solution
|
- A large , heavy box is sliding without friction down a smooth plane o...
Text Solution
|
- An object A is kept fixed at the point x= 3 m and y = 1.25 m on a pl...
Text Solution
|
- On a frictionless horizontal surface , assumed to be the x-y plane ,...
Text Solution
|