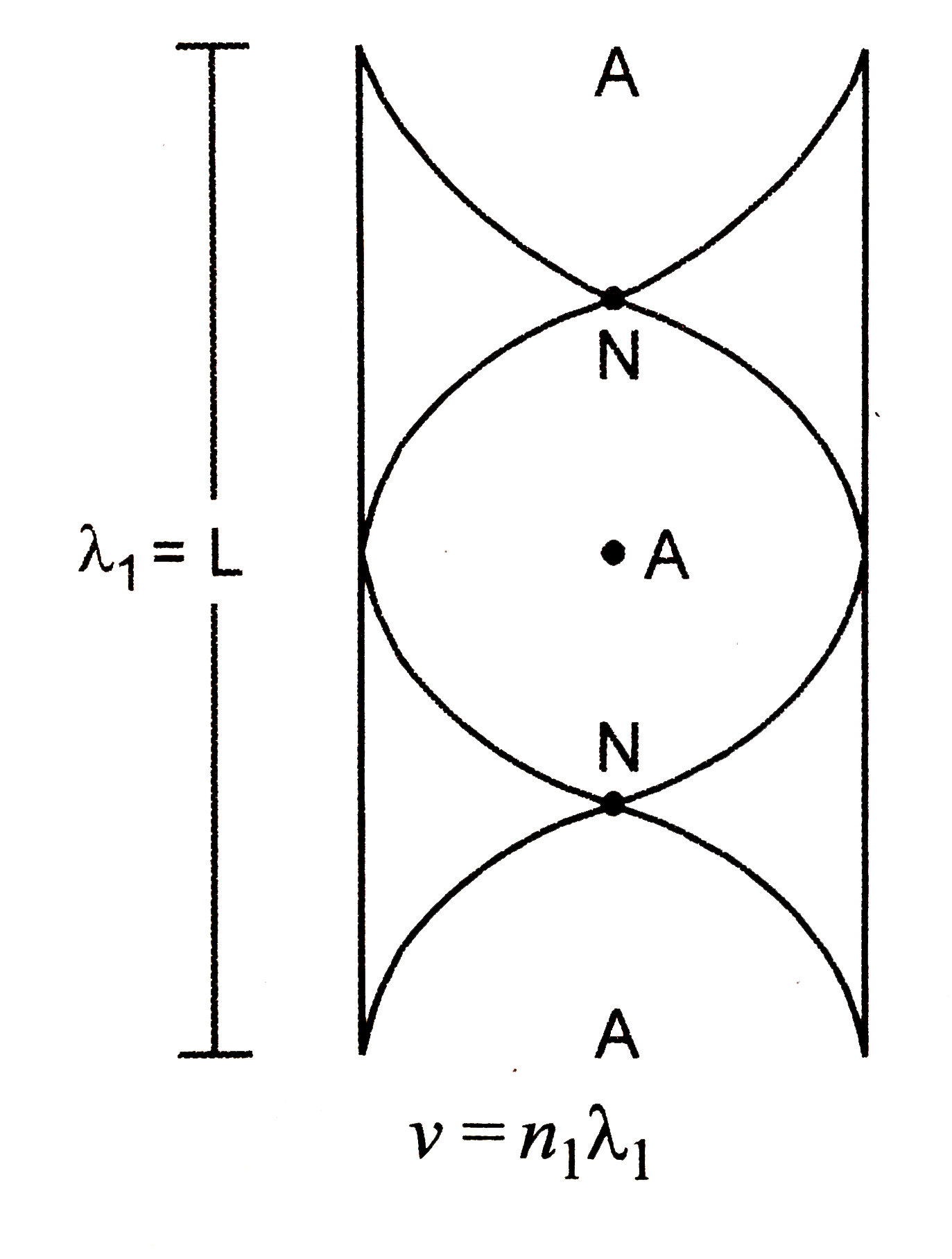
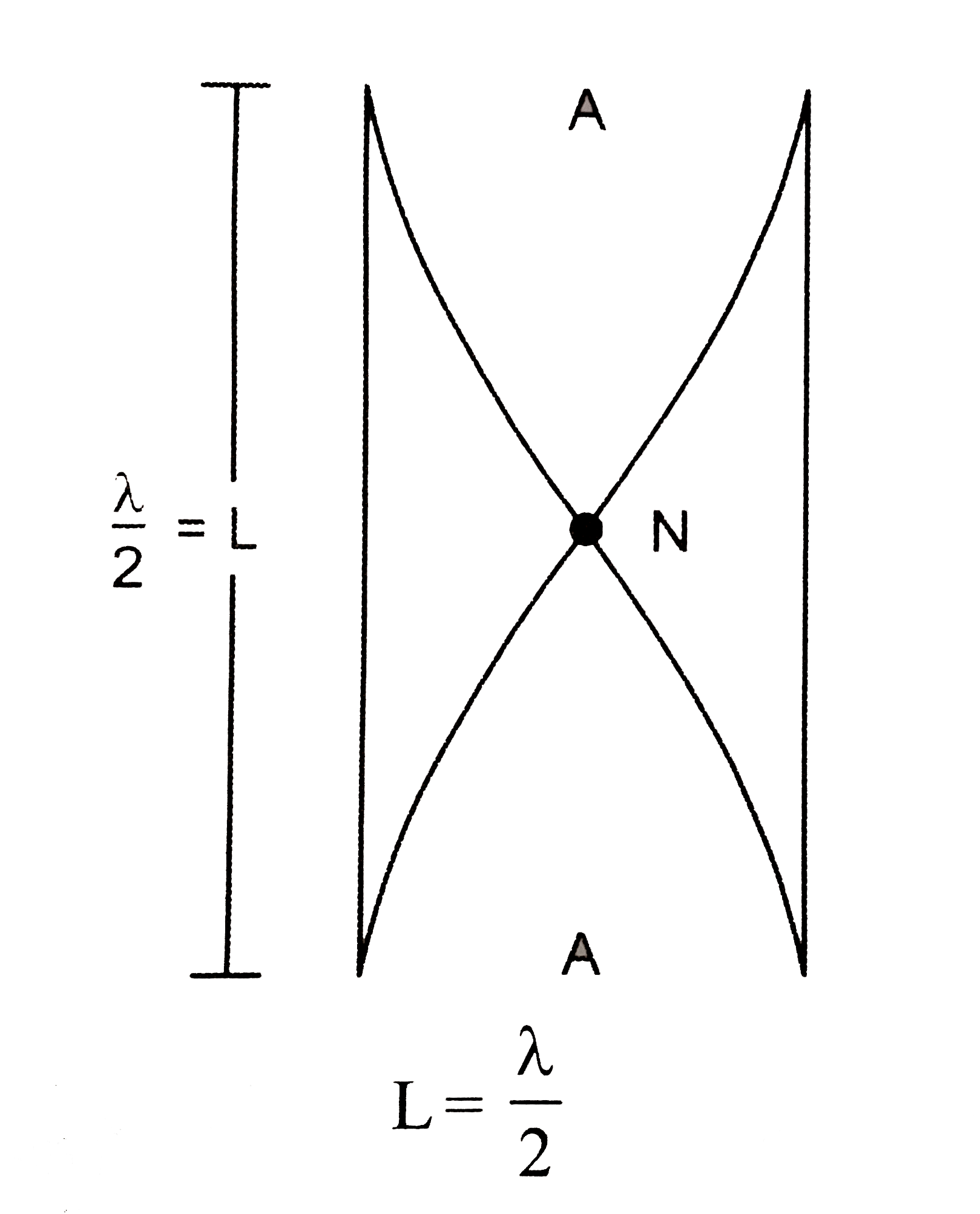Text Solution
Verified by Experts
Topper's Solved these Questions
GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS- FEBRUARY 2019-SECTION-D
- Show that even as well as odd harmonics are present as overtones in th...
Text Solution
|
- Explain the formation of stationary waves by analytical method. Shwo t...
Text Solution
|
- Obtain an expression for potential of a particle performing S.H.M. Wha...
Text Solution
|
- From differential equation of linear S.H.M obtain an expression for ac...
Text Solution
|
- Explain refraction of light the basis of wave theory : Hence prove the...
Text Solution
|
- State Brewster law and show that when light is incident at polarzing a...
Text Solution
|