Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
WORK, ENERGY & POWER
DC PANDEY|Exercise TYPE2|1 VideosView PlaylistWORK, ENERGY & POWER
DC PANDEY|Exercise Miscellaneous Example|6 VideosView PlaylistWORK, ENERGY & POWER
DC PANDEY|Exercise Level 2 Comprehension Based|2 VideosView PlaylistWAVE MOTION
DC PANDEY|Exercise Integer Type Question|11 VideosView PlaylistWORK, ENERGY AND POWER
DC PANDEY|Exercise MEDICAL ENTRACES GALLERY|33 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY-WORK, ENERGY & POWER-Solved Examples
- In the figure shown, all surfaces are smooth and force constant of spr...
01:46
|
Playing Now - A smooth narrow tube in the form of an arc AB of a circle of centre O ...
02:57
|
Play - One end of a light spring of natural length d and spring constant k is...
07:13
|
Play - In the adjoining figure, block A is of mass (m) and block B is of mass...
11:06
|
Play - . In the figure shown, AB = BC = 2m. Friction coefficient everywhere...
08:03
|
Play - A particle slides along a track with elevated ends and a flat central ...
06:44
|
Play - A 0.5kg block slides from the point A on a horizontal track with an in...
06:49
|
Play - A body is desplaced from origin to (2m, 4m) under the following two fo...
05:59
|
Play - A force F=-k(^hati + x^hatj) (where k is a positive constant) acts on ...
03:34
|
Play - A body is displaced from prigin to (1m,1m) by force F=(2yhati + 3x^(...
05:36
|
Play - A particle, which is constrained to move along x-axis, is subjected to...
05:56
|
Play - A particle is placed at the origin and a force F=Kx is acting on it (w...
01:18
|
Play
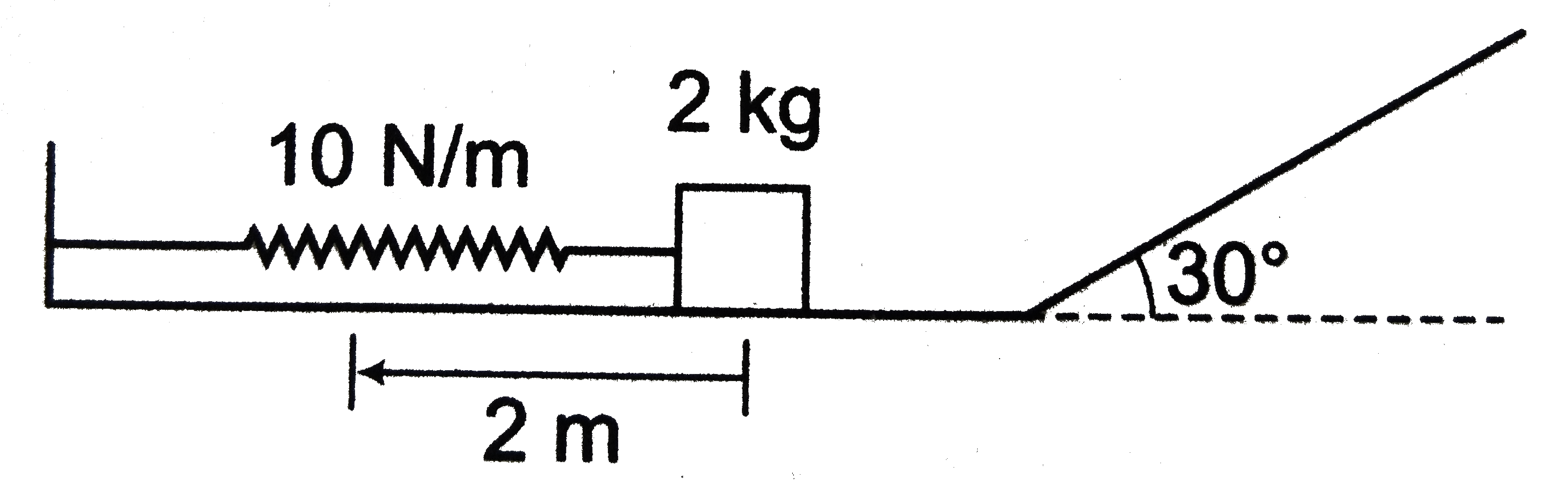 .
.