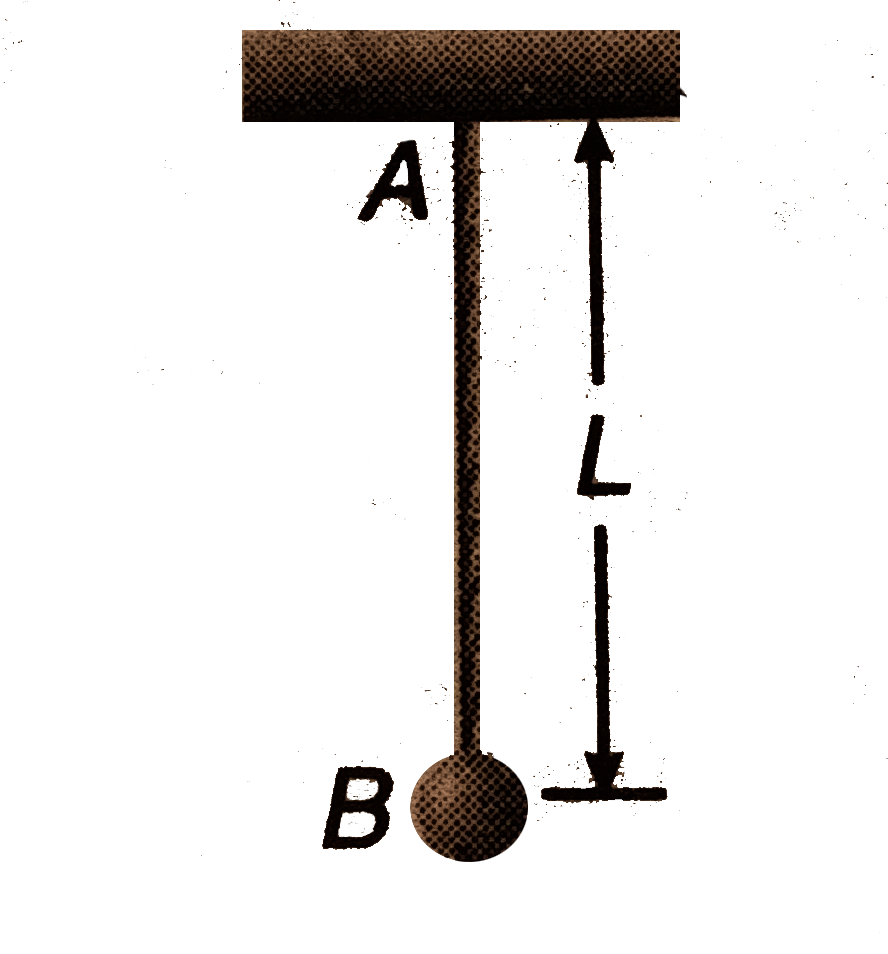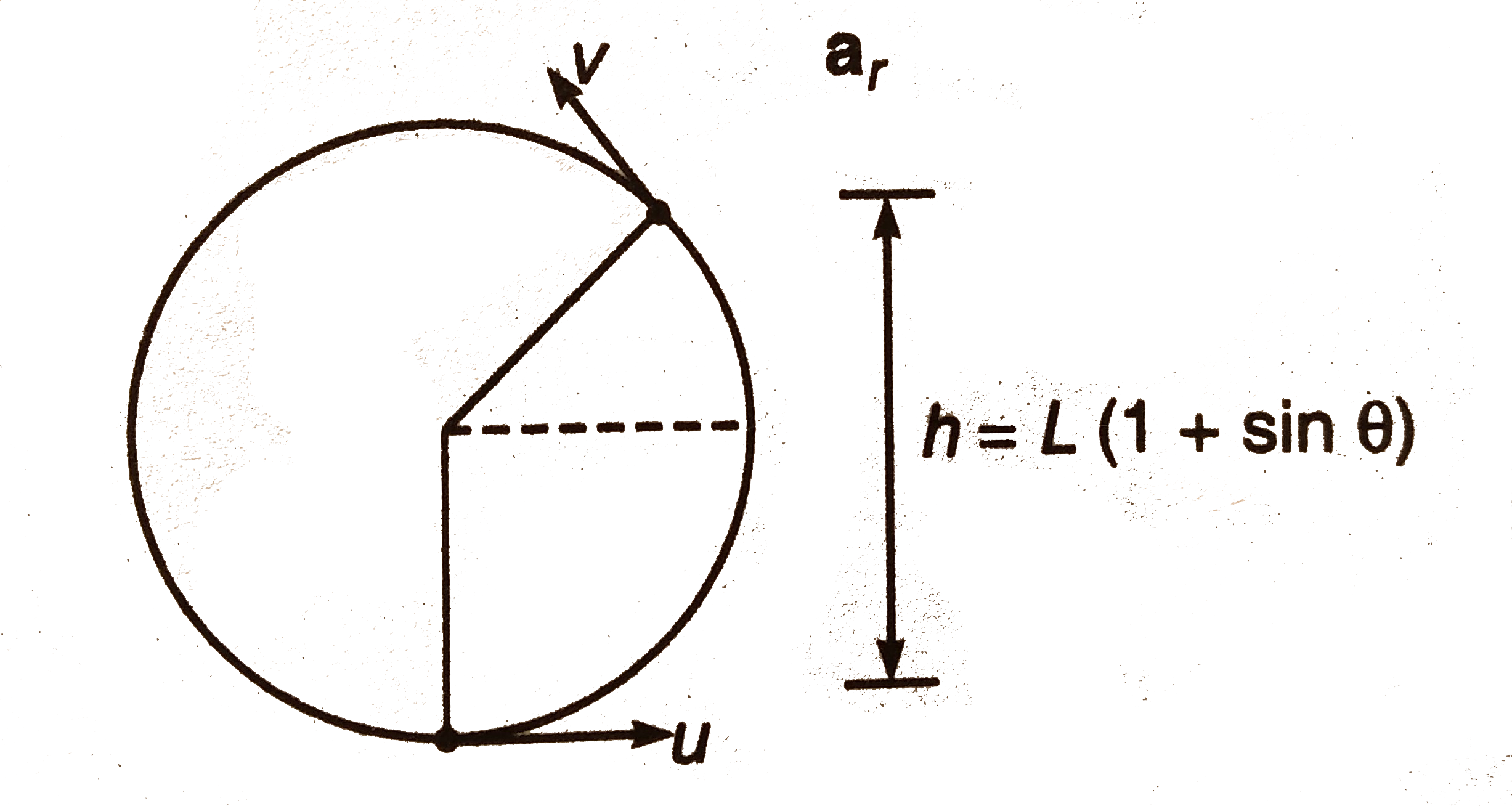Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCULAR MOTION
DC PANDEY|Exercise Subjective Questions|2 VideosCIRCULAR MOTION
DC PANDEY|Exercise JEE Main|23 VideosCIRCULAR MOTION
DC PANDEY|Exercise Level 2 Comprehension Based|5 VideosCENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
DC PANDEY|Exercise Level 2 Subjective|21 VideosCOMMUNICATION SYSTEM
DC PANDEY|Exercise Only One Option is Correct|27 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-CIRCULAR MOTION-Level 2 Subjective
- Bob B of the pendulum AB is given an initial velocity sqrt(3Lg) in hor...
Text Solution
|
- A small sphere B of mass m is released form rest in the position shown...
Text Solution
|
- A particle of mass m is suspended by a string of length l from a fixed...
Text Solution
|
- A turn of radius 20 m is banked for the vehicles going at a speed of ...
Text Solution
|
- What is the radius of curvature of the parabola traced out by the proj...
Text Solution
|
- A particle is projected with velocity 20sqrt(2)m//s at 45^(@) with hor...
Text Solution
|
- If the system shown in the figure is rotated in a horizontal circle wi...
Text Solution
|
- The simple 2Kg pendulum is released from rest in the horizontal positi...
Text Solution
|
- A circular tube of mass M placed veticlly on a horizontal surface as s...
Text Solution
|
- A table with smooth horizontal surface is turning at an angular speed ...
Text Solution
|
- A block of mass m slides 0n a frictionless table. It is constrained to...
Text Solution
|
- A ring of mass M hangs from a thread and two beads of mass m slides on...
Text Solution
|
- A smooth circular tube of radius R is fixed in a vertical plane. A pa...
Text Solution
|