Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
FLUID MECHANICS
DC PANDEY|Exercise Solved Examples|21 VideosView PlaylistFLUID MECHANICS
DC PANDEY|Exercise Miscellaneous Examples|10 VideosView PlaylistEXPERIMENTS
DC PANDEY|Exercise Subjective|15 VideosView PlaylistGENERAL PHYSICS
DC PANDEY|Exercise INTEGER_TYPE|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
DC PANDEY-FLUID MECHANICS-Medical entranes gallery
- A liquid of density rho is in a bucket that spins with angular velocit...
04:56
|
Playing Now - A rectangular film of liquid is extended from (4 cm xx 2 cm) to (5 cm ...
01:51
|
Play - Three liquids of densities rho(1), rho(2) and rho(3) (with rho(1) gt r...
02:29
|
Play - Two non-mixing liquids of densities rho and (n gt1) are put in a cont...
04:31
|
Play - A wind with speed 40m//s blows parallel to the roof of a house. The ar...
02:49
|
Play - The approximate depth of an ocean is 2700m. The compressibility of wat...
02:26
|
Play - Determine the height above the dashed line XX' attained by the water s...
06:45
|
Play - A water drop of radius 10^-2 m is brokenn into 1000 equal droplets. Ca...
05:57
|
Play - The lower end of a capillary tube is dipped into water and it is seen ...
02:35
|
Play - A soap bubble of diameter a is produced using the soap solution of sur...
01:51
|
Play - A boat floating in a water tank is carrying a number of large stones. ...
03:04
|
Play - Choose the correct statement.
Text Solution
|
Play - A 20 cm long capillary tube is dipped vertically in water and the liqu...
01:30
|
Play - By sucking a straw a student can reduce the pressure in his lungs to 7...
03:44
|
Play - What is ratio of surface energy of 1 small drop and 1 large drop, if 1...
02:14
|
Play - A solid floats such that its 1//3 part is above the water surface. The...
02:12
|
Play - The amount of work done in blowing a soap bubble such that its diamete...
02:21
|
Play - When the temperature increased the angle of contact of a liquid
01:39
|
Play - A bubble is at the bottom of the lake of depth h. As the bubble comes ...
03:35
|
Play - A wooden block is floating on water kept in a beaker. 40% of the block...
09:47
|
Play - A small metal sphere of radius a is falling with a velocity upsilon th...
03:50
|
Play
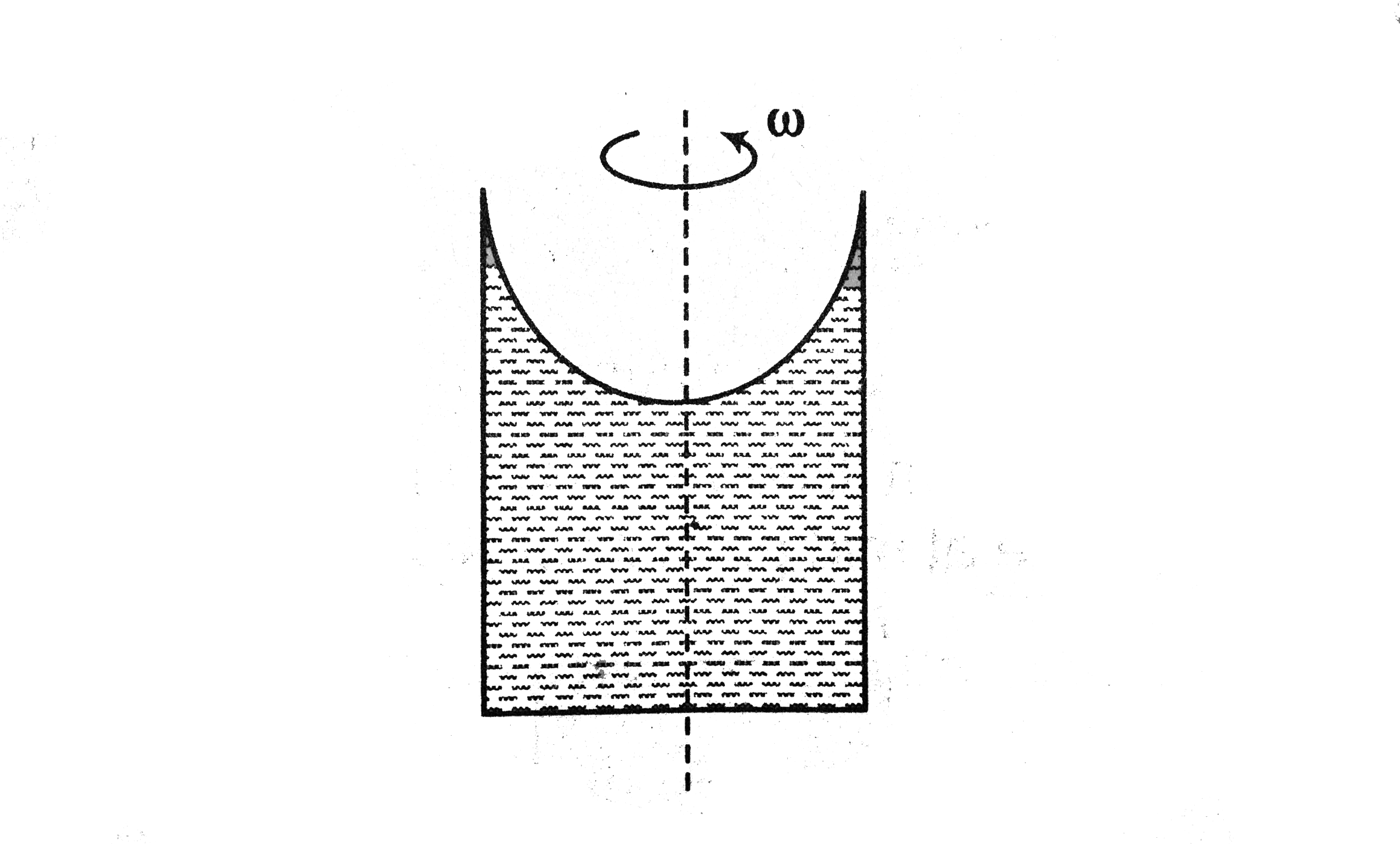 .
.