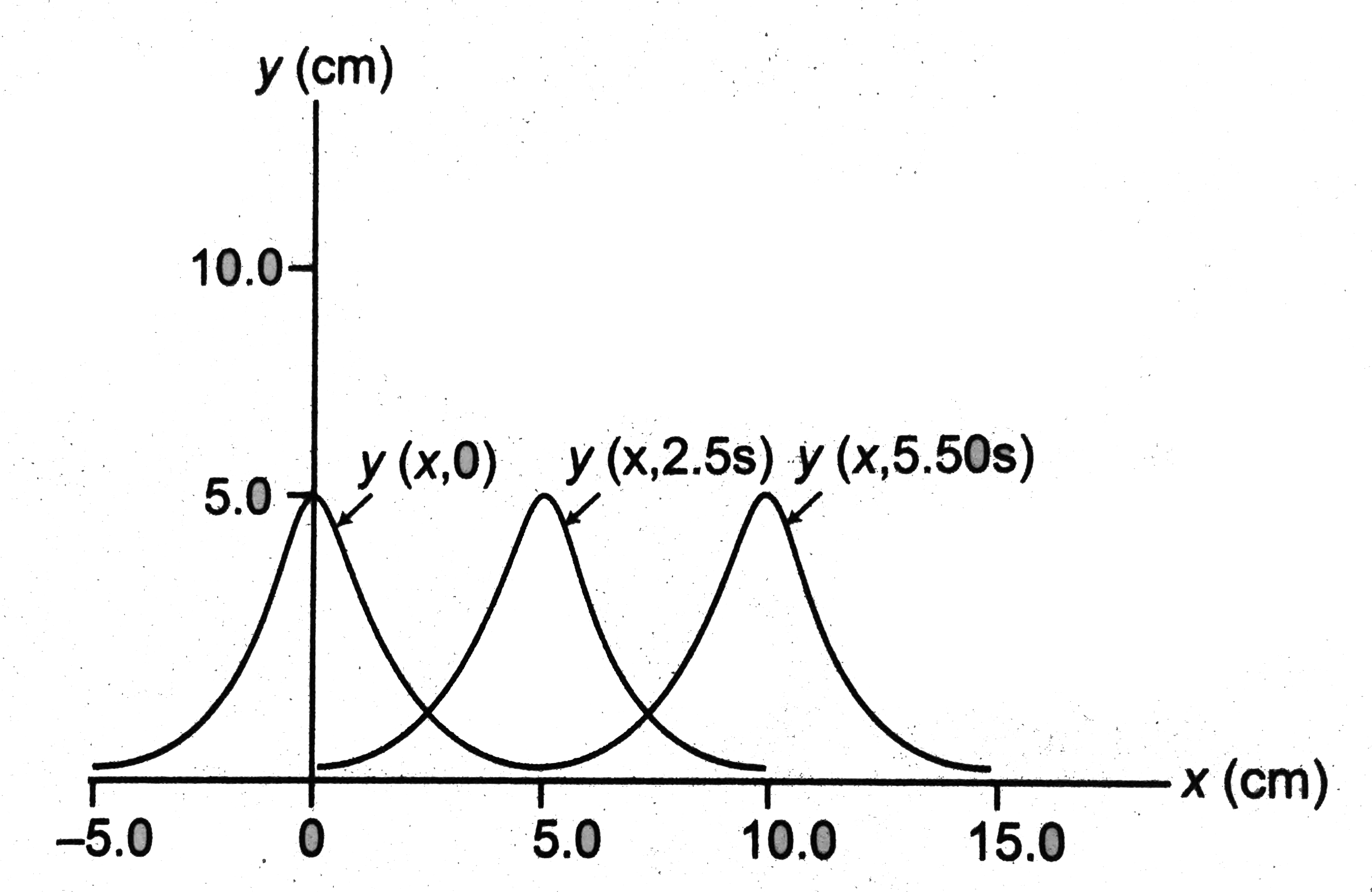Text Solution
Verified by Experts
|
Topper's Solved these Questions
WAVE MOTION
DC PANDEY|Exercise Exercise 17.1|4 VideosView PlaylistWAVE MOTION
DC PANDEY|Exercise Exercise 17.2|2 VideosView PlaylistWAVE MOTION
DC PANDEY|Exercise Example Type 5|1 VideosView PlaylistVECTORS
DC PANDEY|Exercise Medical enrances gallery|9 VideosView PlaylistWORK, ENERGY & POWER
DC PANDEY|Exercise Level 2 Comprehension Based|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY-WAVE MOTION-Miscellaneous Examples
- A block of mass M = 2kg is suspended from a string AB of mass 6 kg as...
02:21
|
Play - A wave moves with speed 300 m//s on a wire which is under a tension of...
02:04
|
Play - For a wave described by y = A sin (omegat - kx), consider the followin...
06:58
|
Play - A thin string is held at one end and oscillates so that, y(x = 0, t...
04:00
|
Play - Consider a wave propagating in the negative x-direction whose frequenc...
04:02
|
Play - A simple harmonic wave of amplitude 8 units travels along positive x-a...
06:09
|
Play - A wave pulse on a horizontal string is represented by the function y...
03:03
|
Playing Now - A uniform circular hoop of string is rotating clockwise in the absence...
04:18
|
Play - A sinusoidal wave trsvelling in the positive direction on a stretched ...
03:44
|
Play