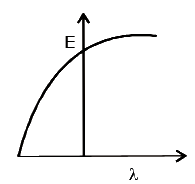
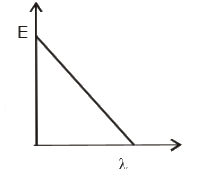
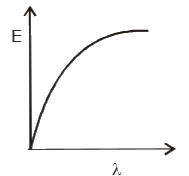
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
MODERN PHYSICS - 1
DC PANDEY|Exercise Level 1 Subjective|40 VideosView PlaylistMODERN PHYSICS - 1
DC PANDEY|Exercise Level 2 Single Correct|22 VideosView PlaylistMODERN PHYSICS - 1
DC PANDEY|Exercise Level -1 Assertion And Reason|10 VideosView PlaylistMODERN PHYSICS
DC PANDEY|Exercise Integer Type Questions|17 VideosView PlaylistMODERN PHYSICS - 2
DC PANDEY|Exercise Level 2 Subjective|10 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY-MODERN PHYSICS - 1-Level 1 Objective
- What is the energy of a hydrogen atom in the first excited state if th...
04:29
|
Play - Light of wavelength 330nm falling on a piece of metal ejects electrons...
03:13
|
Play - Maximum kinetic energy of a photoelectron is E when the wavelength of ...
01:41
|
Playing Now - if the frequency fo Ka X-ray emitted from the element with atomic numb...
02:12
|
Play - According to Mseley's law, the ratio of the slope of graph between sqr...
02:47
|
Play - if the electron in hydrogen orbit jumps form third orbit to second or...
01:11
|
Play - A potential of 10000 V is applied across an x-ray tube. Find the ratio...
03:24
|
Play - When a metallic surface is illuminated with monochromatic light of wav...
01:49
|
Play - The threshold frequency for a certain photosensitive metal is v0. When...
01:45
|
Play - The frequency of the first line in Lyman series in the hydrogen spect...
01:51
|
Play - Which enrgy state of doubly ionized lithium (Li^(++) has the same ener...
01:05
|
Play - Two identical photo-cathodes receive light of frequencies v1 and v2. ...
01:37
|
Play - The longest wavelength of the Lyman series for hydrogen atom is the sa...
01:53
|
Play - The wavelength of the Ka line for the uranium is (Z = 92) (R = 1.0973x...
01:33
|
Play - The frquencies of Kalpha, Kbeta and Lalpha X-rays of a materail are ga...
01:02
|
Play - A proton and an alpha - particle are accelerated through same potentia...
02:46
|
Play - If E1, E2 and E3 represent respectively the kinetic energies of an el...
01:40
|
Play - if the potential energy of a hydrogen atom in the ground state is assu...
00:57
|
Play - A 1000 W transmitter works at a frequency of 880kHz. The number of pho...
01:27
|
Play - Electromagnetic radiation of wavelength 3000 Å is incident on an isola...
01:45
|
Play