Text Solution
Verified by Experts
Topper's Solved these Questions
CIRCLE
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise ASSIGNMENT 4.5|8 VideosCIRCLE
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE|40 VideosCIRCLE
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise ASSIGNMENT 4.3|11 VideosCHALLENGING QUESTIONS
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :|1 VideosCOORDINATE GEOMETRY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignment 6.5|13 Videos
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-CIRCLE-ASSIGNMENT 4.4
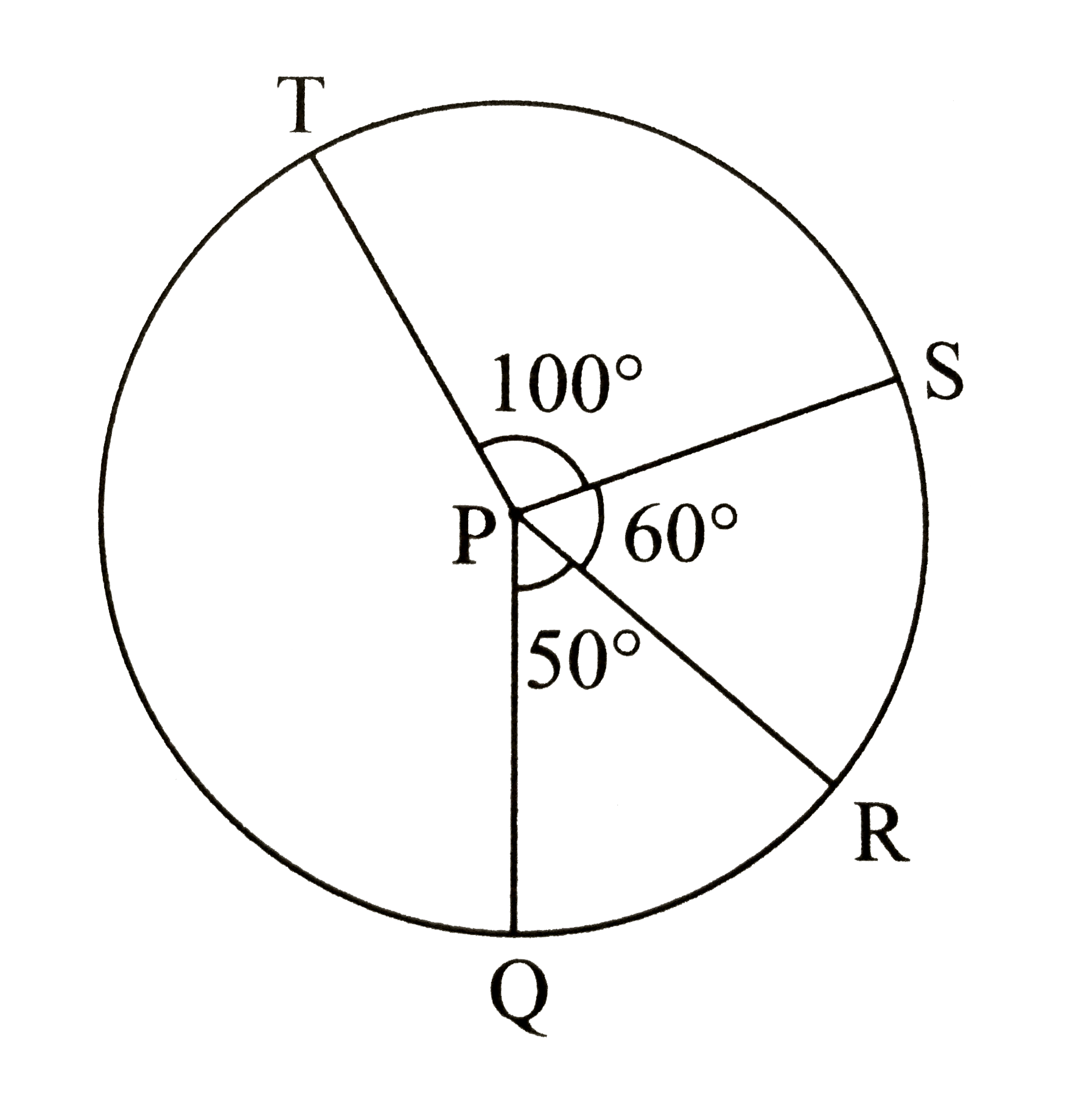
- In the figure, P is the cnetre of the circle. If / QPR 50^(@), / RPS ...
Text Solution
|
- In the figure, if / ADC = / CBP then prove that square ABCD is cycli...
Text Solution
|
- square ABCD is a cyclic quadrilateral in which AB = AD ./BCD = 70^(@)...
Text Solution
|
- square ABCD is a rectangle. Taking AD as a diameter a semicircle AXD i...
Text Solution
|
- Circles with centres A,B,C and radius 5 cm each, touch each other exte...
Text Solution
|
- In the figure, diameter AB and chord CD intersect in point E. If m (...
Text Solution
|
- In the figure, m ( arc NS ) = 130^(@) m (arc EF ) = 60^(@). Find (...
Text Solution
|
- In the figure, two chords AB and CD are parallel to each other. P is ...
Text Solution
|
- square ABCD is a cyclic quadrilateral, m (arc ABC) = 220^(@) then fin...
Text Solution
|
- In the figure, O is the centre of the circle and B is a point of conta...
Text Solution
|
- In the figure , O is the radius of the circle. From point R, seg RM an...
Text Solution
|
- In the figure , circles with centres X and Y touch internally at poin...
Text Solution
|