Home
Class 10
MATHS
In the above figure, seg AB is a diamete...


In the above figure, seg AB is a diameter of a circle with centre P.C is any point on the circle. Seg CE `_|_` seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of folloing steps:
(a) Draw ray CE. It intersects the circle at D.
(b) Show that CE = ED.
Write the result using theorem of intersection of chords insides a circle.
(d) Using CE = ED, complete the proof.

Text Solution

Verified by Experts


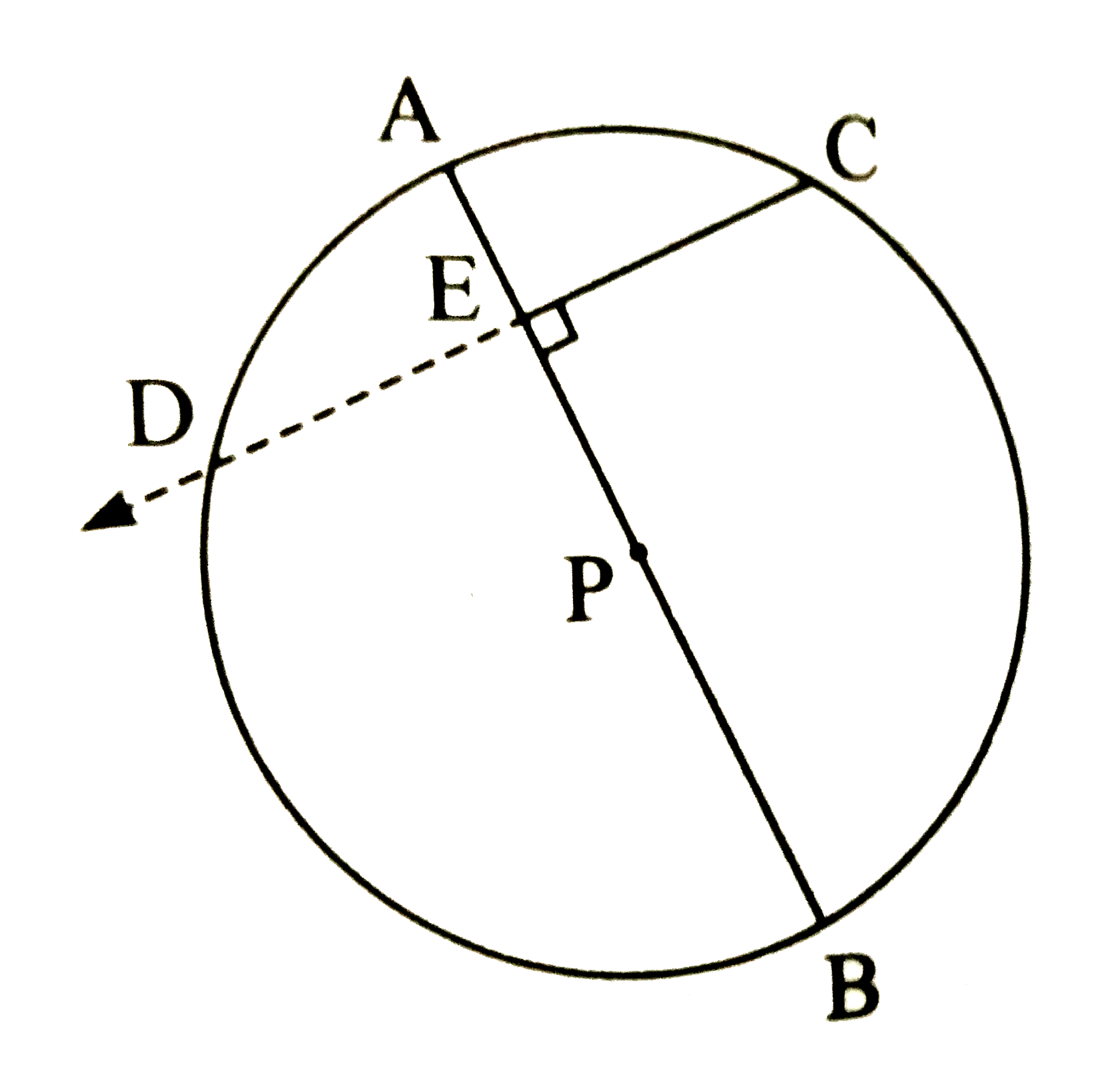
In circle with centre p,AB is a diameter and seg CE `_|_` seg AB ….(Given)
`:.` seg PE `_|_` chord CD (Construction)
`:.` sec CE `~=` seg DE….(i)
(Perpendicular drawn from centre of the circle to the chord bisects the chord)
seg AB and seg CD are two chords intersecting inside the circle a point E
`:. AE xx BE = CE xx DE`
(Theorem of internal division of chords)
`AE xx BE = CE xx CE` .... (From i)
`AE xx BE = CE^(2)`
`:. CE^(2) = AE xx BE`
Hence it is proved that CE is the geometric mean of AE and EB.
Promotional Banner

Topper's Solved these Questions

  • MODEL QUESTION PAPER

    NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise SOLVE ANY TWO THE FOLLOWIN SUBQUESTIONS:|3 Videos

  • MENSURATION

    NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignment 8.5|8 Videos

  • PRACTICE QUESTION BASED

    NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise STATISTICS|13 Videos

Similar Questions

Explore conceptually related problems

In figure, seg RS is a diameter of the circle with centre O. Point T lines in the exterior of the circle. Prove that /_RTS is an acute angle.

In the adjoining figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that angleRTS is an acute angle.

In the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of angleACB intersects the circle at point D. Prove that ,seg ADcongseg BD . Complete the following proof by filling the blanks.

In figure, seg AB is a diameter of a circle with centre O. The bisector of /_ACB intersects the circle at point D. Prove that seg AD cong seg BD. Complete the following proof by filling in the blanks

In the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP _|_ line PQ and seg BQ _|_ line PQ. Prove that, seg CP ~= seg CQ.

In the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP bot line PQ and seg BQ bot line PQ. Prove that, seg CP cong seg CQ.

In the figure , seg AB is the chord of the circle with centre O. if AM =4 cm then find MB and AB. State your reason.

In the adjoining figure , seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DEtimesGE=4r^2 .

In figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DExxGE=4r^(2) .